Cho số phức z thỏa mãn \(\left| z-2+3i \right|+\left| z+2+i \right|=4\sqrt{5}\). Tính GTLN của \(P=\left| z-4+4i \right|\)

Cho số phức \(z=x+yi,\,\,\left( x,y\in R \right)\), \(S(x;y)\)là điểm biểu diễn của z trên hệ trục tọa độ Oxy.

\(\left| z-2+3i \right|+\left| z+2+i \right|=4\sqrt{5}\Leftrightarrow \sqrt{{{(x-2)}^{2}}+{{(y+3)}^{2}}}+\sqrt{{{(x+2)}^{2}}+{{(y+1)}^{2}}}=4\sqrt{5}\,\)(1)

Lấy các điểm \(A(2;-3),\,\,B(-2;-1)\). Phương trình (1) \(\Leftrightarrow SA+SB=4\sqrt{5}\)

\(\Rightarrow \) Tập hợp các điểm S là đường elip (E) có tiêu điểm \(A(2;-3),\,\,B(-2;-1)\) và có độ dài trục lớn là \(2a=4\sqrt{5}\Rightarrow a=2\sqrt{5}\).

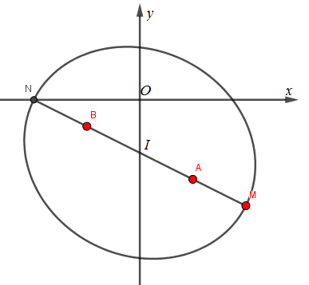
Lấy \(M(4;-4)\). Dễ dàng kiểm tra được \(\left\{ \begin{align}  & \overrightarrow{AB}=2\overrightarrow{MA} \\ & MA+MB=4\sqrt{5}=2a \\\end{align} \right.\)

Suy ra, M là một đỉnh và nằm trên trục lớn của elip (E).

Gọi I là trung điểm AB \(\Rightarrow I\left( 0;-2 \right)\), N là điểm đối xứng của M qua I. Khi đó, với mọi điểm \(S\in \left( E \right)\): \(SM\le MN=2a=4\sqrt{5}\)

\(S{{M}_{\max }}=4\sqrt{5}\,\,\)khi và chỉ khi S trùng N \(\Leftrightarrow {{P}_{\max }}=4\sqrt{5}\) khi và chỉ khi \(S\equiv N(-4;0)\Leftrightarrow z=-4\)