Câu hỏi:
2 năm trước
Cho hai số phức \({{z}_{1}},{{z}_{2}}\) thỏa mãn \(\left| {{z}_{1}} \right|=2,\,\,\left| {{z}_{2}} \right|=\sqrt{3}\). Gọi M, N là các điểm biểu diễn cho \({{z}_{1}}\) và \(i{{z}_{2}}\). Biết \(\widehat{MON}={{30}^{0}}\). Tính \(S=\left| z_{1}^{2}+4z_{2}^{2} \right|\) ?
Trả lời bởi giáo viên
Đáp án đúng: b
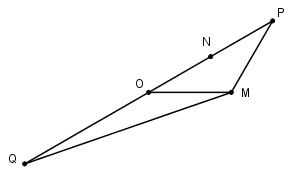
Đặt \({{z}_{3}}=i{{z}_{2}}\Rightarrow z_{3}^{2}=-z_{2}^{2}\Rightarrow S=\left| z_{1}^{2}+4z_{2}^{2} \right|=\left| z_{1}^{2}-4z_{3}^{2} \right|=\left| {{z}_{1}}-2{{z}_{3}} \right|\left| {{z}_{1}}+2{{z}_{3}} \right|\)M, N là các điểm biểu diễn cho \({{z}_{1}},{{z}_{3}}\Rightarrow OM=2,\,\,ON=\left| {{z}_{3}} \right|=\left| i{{z}_{2}} \right|=\left| i \right|.\left| {{z}_{2}} \right|=\sqrt{3}\).Gọi P là điểm biểu diễn cho \(2{{z}_{3}}\) và \(Q\) là điểm biểu diễn cho \(-2{{z}_{3}}\) , ta có N là trung điểm của OP và P, Q đối xứng nhau qua O. Khi đó \(S=MP.MQ\).
Áp dụng định lí Cosin trong \(\Delta OMP\) có:
\(M{{P}^{2}}=O{{P}^{2}}+O{{M}^{2}}-2OP.OM.\cos 30=12+4-2.2\sqrt{3}.2.\dfrac{\sqrt{3}}{2}=4\Rightarrow MP=2\)Áp dụng định lí Cosin trong \(\Delta OMQ\) có:
\(\begin{align} M{{Q}^{2}}=O{{M}^{2}}+O{{Q}^{2}}-2OM.OQ.\cos {{150}^{0}} \\ \,\,\,\,\,\,\,\,\,\,\,\,=4+12+2.2.2\sqrt{3}.\dfrac{\sqrt{3}}{2}=2\sqrt{7} \\ \Rightarrow S=MP.MQ=2.2\sqrt{7}=4\sqrt{7} \\ \end{align}\)
Hướng dẫn giải:
Tìm các điểm biểu diễn và đưa về bài toán hình học.
Câu hỏi khác
- Bài tập số phức và các phép toán cộng, trừ, nhân, chia số phức toán 12 có lời giải
- Bài tập phương trình bậc hai với hệ số thực (căn bậc hai của số phức) toán 12 có lời giải
- Bài tập tìm min, max liên quan đến số phức có lời giải MÔN TOÁN Lớp 12
- Bài tập điểm biểu diễn số phức thỏa mãn điều kiện cho trước có lời giải MÔN TOÁN Lớp 12
- Bài tập dạng lượng giác của số phức toán 12 có lời giải
