Cho hai số phức \({{z}_{1}};{{z}_{2}}\) thỏa mãn điều kiện \(2\left| \overline{{{z}_{1}}}+i \right|=\left| \overline{{{z}_{1}}}-{{z}_{1}}-2i \right|\) và \(\left| {{z}_{2}}-i-10 \right|=1\). Tìm giá trị nhỏ nhất của biểu thức \(\left| {{z}_{1}}-{{z}_{2}} \right|\) ?

Gọi \({{z}_{1}}=x+yi\) ta có:

\(2\left| x-yi+i \right|=\left| x-yi-x-yi-2i \right| \) \(\Leftrightarrow 2\left| x-yi+i \right|=2\left| yi+i \right|\) \(\Leftrightarrow {{x}^{2}}+{{\left( y-1 \right)}^{2}}={{\left( y+1 \right)}^{2}}\) \(\Leftrightarrow {{x}^{2}}+{{y}^{2}}-2y+1={{y}^{2}}+2y+1\) \(\Leftrightarrow {{x}^{2}}=4y\) \(\Leftrightarrow y=\dfrac{{{x}^{2}}}{4}\)
\(\Rightarrow \) Tập hợp các điểm biểu diễn cho số phức \({{z}_{1}}\) là parabol \(y=\dfrac{{{x}^{2}}}{4}\).
Tập hợp các điểm biểu diễn cho số phức \({{z}_{2}}\) là là đường tròn \(\left( C \right)\) tâm \(I\left( 10;1 \right)\) bán kính \(R=1\).
\(\Rightarrow \left( C \right):\,\,{{\left( x-10 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=1\).
Gọi M, N lần lượt là điểm biểu diễn cho số phức \({{z}_{1}},{{z}_{2}}\Rightarrow \left| {{z}_{1}}-{{z}_{2}} \right|=\left| \overrightarrow{OM}-\overrightarrow{ON} \right|=MN\)
\(\Rightarrow {{\left| {{z}_{1}}-{{z}_{2}} \right|}_{\min }}\Leftrightarrow M{{N}_{\min }}\).

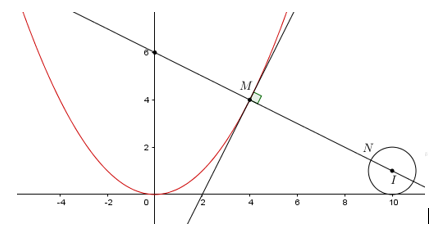
Dựa vào hình vẽ ta thấy \(M{{N}_{\min }}\Leftrightarrow MN\bot \) tiếp tuyến tại M của parabol \(y=\dfrac{{{x}^{2}}}{4}\) và đi qua I.
Ta có \(y'=\dfrac{x}{2}\) . Gọi \(M\left( m;\dfrac{{{m}^{2}}}{4} \right)\,\,\left( m>0 \right)\Rightarrow y'\left( m \right)=\dfrac{m}{2}\Rightarrow pttt:\,\,y=\left( x-m \right)+\dfrac{{{m}^{2}}}{4}=\dfrac{m}{2}x-\dfrac{{{m}^{2}}}{4}\,\,\left( d \right)\)
\(\begin{align} \Rightarrow MN\ge d\left( I;d \right)-1\Rightarrow M{{N}_{\min }}\Leftrightarrow d\left( I;d \right)=IM \\ \Leftrightarrow \dfrac{\left| 5m-1-\dfrac{{{m}^{2}}}{4} \right|}{\sqrt{1+\dfrac{{{m}^{2}}}{4}}}=\sqrt{{{\left( m-10 \right)}^{2}}+{{\left( \dfrac{{{m}^{2}}}{4}-1 \right)}^{2}}} \\ \Leftrightarrow \dfrac{{{\left( 5m-1-\dfrac{{{m}^{2}}}{4} \right)}^{2}}}{1+\dfrac{{{m}^{2}}}{4}}={{\left( m-10 \right)}^{2}}+{{\left( \dfrac{{{m}^{2}}}{4}-1 \right)}^{2}} \\ \end{align}\)
Giải phương trình trên ra tìm được \(m=4\), khi đó \(IM=3\sqrt{5}\Rightarrow M{{N}_{\min }}=3\sqrt{5}-1\) .