Cho hai số phức z, w thỏa mãn \(\left\{ \begin{align}  \left| z-3-2i \right|\le 1 \\  \left| \text{w}+1+2i \right|\le \left| \text{w}-2-i \right| \\ \end{align} \right.\). Tìm GTNN \({{P}_{\min }}\) của biểu thức \(P=\left| z-\text{w} \right|\).

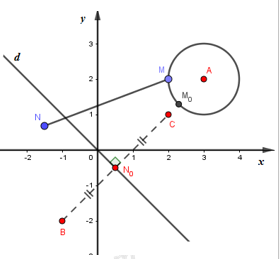
Đặt \(A(3;2),\,\,B(-1;-2),\,\,C(2;1)\). Gọi M, N lần lượt là điểm biểu diến của z, w.

Vì \(\left| z-3-2i \right|\le 1\) nên tập hợp điểm biểu diễn của z trên hệ trục Oxy là hình tròn tâm A bán kính 1.

Vì \(\left| \text{w}+1+2i \right|\le \left| \text{w}-2-i \right|\) nên tập hợp điểm biểu diễn của w trên hệ trục Oxy là nửa mặt phẳng bờ d chứa B và đường thẳng d. Trong đó d là trung trực của đoạn thẳng BC.

\(P=\left| z-\text{w} \right|=MN\), \({{P}_{\min }}=M{{N}_{\min }}\).

Dễ dàng kiểm tra được A, B, C thẳng hàng và MN ngắn nhất khi MN trùng với \({{M}_{0}}{{N}_{0}}\).

Trong đó, \({{N}_{0}}\): trung điểm của BC, \({{M}_{0}}\): giao của AB và đường tròn \(\left( A;1 \right)\).

Độ dài đoạn \({{M}_{0}}{{N}_{0}}=d\left( A;d \right)-R=d(A;d)-1\)

*) Phương trình đường thẳng d:

\({{N}_{0}}\) là trung điểm BC \(\Rightarrow {{N}_{0}}\left( \dfrac{1}{2};\dfrac{-1}{2} \right)\)

\(\overrightarrow{BC}=(3;3)\Rightarrow d\)có 1 VTPT là \(\left( 1;1 \right)\)

Phương trình đường thẳng d: \(1(x-\dfrac{1}{2})+1(y-\dfrac{-1}{2})=0\Leftrightarrow x+y=0\)

\(d\left( A;d \right)=\dfrac{\left| 3+2 \right|}{\sqrt{{{1}^{2}}+{{1}^{2}}}}=\dfrac{5}{\sqrt{2}}\Rightarrow {{M}_{o}}{{N}_{0}}=\dfrac{5}{\sqrt{2}}-1=\dfrac{5\sqrt{2}-2}{2}\)

Vậy, \({{P}_{\min }}=\dfrac{5\sqrt{2}-2}{2}\)