Bảng biến thiên sau đây là của hàm số nào?
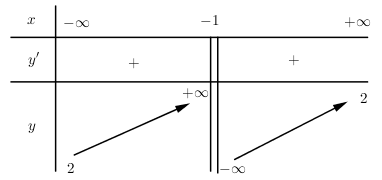
Ta có \(\mathop {\lim }\limits_{x \to - 1} {\mkern 1mu} y = \infty \Rightarrow \) Đồ thị hàm số có tiệm cận đứng là \(x = - 1 \Rightarrow \) Loại đáp án B và D.
\(\mathop {\lim }\limits_{x \to \pm \infty } {\mkern 1mu} y = 2 \Rightarrow \) Đồ thị hàm số có tiệm cận ngang là y = 2 \( \Rightarrow \) Loại đáp án C.
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số dưới đây. Hỏi hàm số đó là hàm số nào?
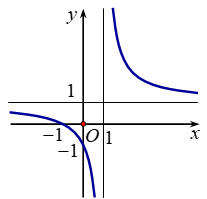
Từ đồ thị suy ra đồ thị hàm số có tiệm cận ngang là \(y=1\) và tiệm cận đứng là \(x=1\) đồng thời đồ thị đi qua điểm \(\left( 0;-1 \right)\) nên chọn đáp án D.
Đường cong ở hình bên là đồ thị hàm số \(y=\dfrac{ax+2}{cx+b}\) với \(a,b,c\) là các số thực. Mệnh đề nào sau đây đúng?
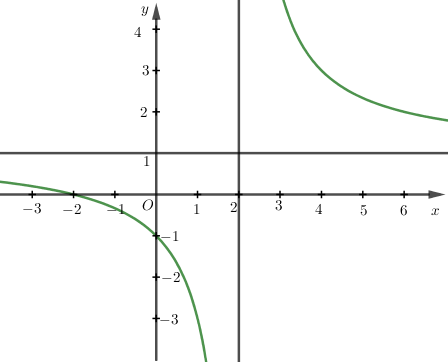
Vì đồ thị hàm số nhận đường thẳng \(y=1;x=2\) làm đường tiệm cận ngang và tiệm cận đứng và đồ thị hàm số cắt \(Oy\) tại điểm có tung độ bằng \(-1\) nên ta có hệ :
\(\left\{ {\begin{array}{*{20}{c}}{ - \dfrac{b}{c} = 2}\\{\dfrac{a}{c} = 1}\\{\dfrac{2}{b} = - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = - 2}\\{c = 1}\end{array}} \right.\).
Cho hàm số \(y=\dfrac{ax+b}{cx+1}\) có bảng biến thiên:
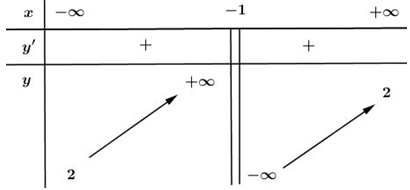
Xét các mệnh đề:
\(\begin{align} & \left( 1 \right)\,\,\,\,\,c=1 \\ & \left( 2 \right)\,\,\,\,a=2 \\ \end{align}\)
(3) Hàm số đồng biến trên \(\left( -\infty ;-1 \right)\cup \left( -1;+\infty \right).\)
(4) Nếu \(y'=\frac{1}{{{\left( x+1 \right)}^{2}}}\) thì \(b=1.\)
Tìm số mệnh đề đúng trong các mệnh đề trên.
TXĐ: \(D=R\backslash \left\{ -\frac{1}{c} \right\}.\)
Ta có: \(y'=\frac{a-bc}{{{\left( cx+1 \right)}^{2}}}.\)
Ta thấy đồ thị có TCĐ \(x=-1\Rightarrow -\frac{1}{c}=-1\Rightarrow c=1\Rightarrow \) Mệnh đề (1) đúng.
Đồ thị hàm số có TCN \(y=2\Rightarrow \frac{a}{c}=2\Leftrightarrow a=2c=2\Rightarrow \) Mệnh đề (2) đúng.
Theo BBT ta thấy hàm số đồng biến trên từng khoảng xác định của hàm số.
\(\Rightarrow y'>0\Leftrightarrow a-bc>0\) do \({{\left( cx+1 \right)}^{2}}>0\,\,\,\forall x\in D \)
\(\Rightarrow \) Hàm số đồng biến trên \(\left( -\infty ;\,\,-1 \right)\) và \(\left( -1;+\infty \right)\Rightarrow \) Mệnh đề (3) sử dụng kí hiệu hợp nên sai.
Nếu \(y'=\frac{1}{{{\left( x+1 \right)}^{2}}}\Rightarrow \frac{a-bc}{{{\left( cx+1 \right)}^{2}}}=\frac{1}{{{\left( x+1 \right)}^{2}}}\)
\(\begin{align} & \Leftrightarrow \frac{2-b}{{{\left( x+1 \right)}^{2}}}=\frac{1}{{{\left( x+1 \right)}^{2}}}\Leftrightarrow 2-b=1 \\ & \Leftrightarrow b=1. \\ \end{align}\)
\(\Rightarrow \) Mệnh đề (4) đúng.
Như vậy có 3 mệnh đề đúng.
Đường cong ở hình bên là đồ thị hàm số \(y = {{ax + b} \over {cx + d}}\) , với a, b, c, d là các số thực. Mệnh đề nào dưới đây đúng?
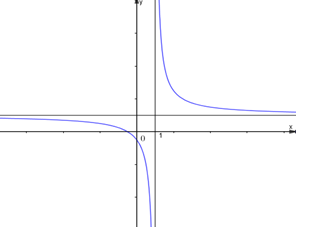
Ta có x = 1 là tiệm cận đứng của đồ thị hàm số nên TXĐ của hàm số là \(D = R\backslash \left\{ 1 \right\}\)
Hàm số liên tục trên \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\)
Theo chiều tăng của x, ta thấy đồ thị hàm số đi xuống trên toàn bộ TXĐ, tức là y giảm, do đó hàm số nghịch biến trên TXĐ của nó.
Đề thi THPT QG - 2021 - mã 101
Biết hàm số \(y = \dfrac{{x + a}}{{x + 1}}\,\,(a\) là số thực cho trước, \(a \ne 1\)) có đồ thị như trong hình bên. Mệnh đề nào dưới đây đúng?
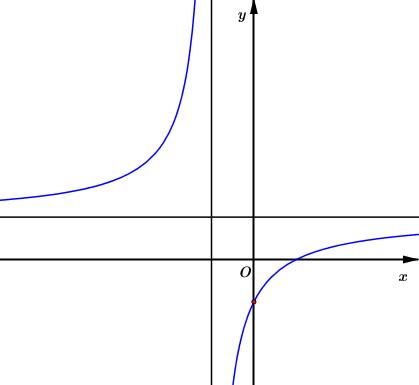
+ Từ đồ thị ta nhận thấy hàm số đồng biến trên mỗi khoảng xác định \( \Rightarrow y' > 0\).
+ Do hàm số \(y = \dfrac{{x + a}}{{x + 1}}\) không xác định tại \(x = - 1\) \( \Rightarrow y' > 0\,\,\forall x \ne - 1\).
Mệnh đề nào dưới đây là sai khi nói về hàm số \(y = \dfrac{{x - 1}}{{x + 1}}?\)
Xét hàm số \(y = \dfrac{{x - 1}}{{x + 1}}\) có TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\)
Ta có \(y' = \dfrac{2}{{{{\left( {x + 1} \right)}^2}}} > 0\) nên hàm số đồng biến trên từng khoảng xác định hay hàm số không có cực trị. Do đó C sai. Và hàm số không có giá trị nhỏ nhất trên toàn tập xác định của nó nên D đúng.
Đồ thị hàm số nhận \(y = 1\) làm TCN và \(x = - 1\) làm TCĐ nên A đúng.
Thay \(x = 1;y = 0\) vào hàm số ta được \(0 = \dfrac{{1 - 1}}{{1 + 1}} \Leftrightarrow 0 = 0\) (luôn đúng) nên điểm \(A\left( {1;0} \right)\) thuộc đồ thị hàm số, do đó B đúng.
Hình sau là đồ thị của hàm số \(y = \dfrac{{ax + b}}{{x + c}}\) (với \(a,b,c \in \mathbb{R}\)).
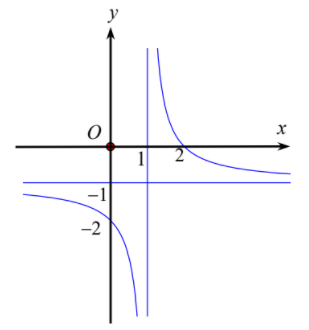
Khi đó \(ab - c\) bằng
Bước 1: Tính giới hạn của hàm số tại vô cực để tính a, tìm đường tiệm cận đứng, từ đó tìm c
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = - 1 \Rightarrow \dfrac{a}{1} = - 1 \Rightarrow a = - 1\)
\(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty \Rightarrow c = - 1\)
Bước 2: Thay tọa độ điểm (0;-2) vào hàm số tìm b, tính ab-c.
Thay tọa độ của (0;-2) vào ta được:
\( - 2 = \dfrac{b}{c} \Rightarrow b = - 2c = 2\)
\( \Rightarrow ab - c = - 1\)
Đề thi THPT QG - 2021 - mã 102
Biết hàm số \(y = \dfrac{{x + a}}{{x + 1}}\) ( \(a\) là số thực cho trước, \(a \ne 1\)) có đồ thị như trong hình bên. Mệnh đề nào dưới đây đúng?
Ta có đồ thị hàm số có phần đường cong đi xuống nên \(y' < 0\) với \(x \ne - 1\)
Cho hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có đồ thị là đường cong trong hình vẽ bên. Kết luận nào sau đây đúng?
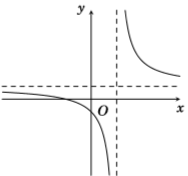
Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có TCN \(y = \dfrac{a}{c}\), TCĐ \(x = - \dfrac{d}{c}\).
Dựa vào đồ thị hàm số ta thấy \(\dfrac{a}{c} > 0 \Leftrightarrow ac > 0\), \( - \dfrac{d}{c} > 0 \Leftrightarrow cd < 0\).
\( \Rightarrow ac.cd < 0 \Leftrightarrow ad.{c^2} < 0 \Leftrightarrow ad < 0\), do đó loại đáp án A và D.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên thay \(x = 0\) ta có \(\dfrac{b}{d} < 0 \Leftrightarrow bd < 0\).
\( \Rightarrow cd.bd > 0 \Leftrightarrow bc.{d^2} > 0 \Leftrightarrow bc > 0\), loại đáp án C.
Vậy \(ad < 0,\,\,bc > 0\).
Đồ thị hàm số nào dưới đây có dạng như đường cong ở hình bên dưới?
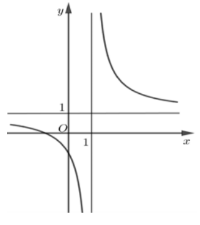
Dựa vào đồ thị hàm số, ta thấy đồ thị hàm số có TCĐ là \(x = 1 \Rightarrow \) loại đáp án C và D.
Đồ thị hàm số có TCN là \(y = 1 \Rightarrow \) loại đáp án B.
Đường cong trong hình vẽ là đồ thị hàm số nào dưới đây?
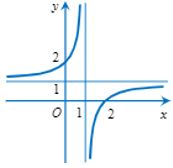
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có TCĐ là \(x = 1\) \( \Rightarrow \) loại đáp án C và D.
Đồ thị hàm số đi qua điểm \(\left( {2;\,\,0} \right)\)
Thay x=2 vào đáp án A ta thấy y=0 nên đồ thị hàm số ở đáp án A đi qua (2;0) (thỏa mãn).
Thay x=2 vào đáp án B ta thấy y=4/3 nên loại B.
Tâm đối xứng của đồ thị hàm số \(y = \dfrac{{x - 1}}{{x + 1}}\) có tọa độ là
Xét hàm số: \(y = \frac{{x - 1}}{{x + 1}}\) có TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}.\)
Ta có: Đồ thị hàm số có TCĐ: \(x = - 1\) và TCN: \(y = 1.\)
\( \Rightarrow I\left( { - 1;\,\,1} \right)\) là tâm đối xứng của đồ thị hàm số.
Đường cong trong hình vẽ là đồ thị của hàm số nào trong bốn hàm số sau
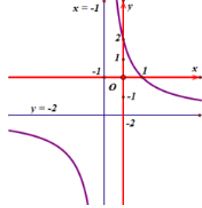
Ta có từ đồ thị hàm số ta thấy hàm số giảm, có tiệm cận ngang là \(y = - 2\) nên loại đáp án A, C và D.
Cho hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\)\(\left( {d < 0} \right)\) có đồ thị như hình bên. Khẳng định nào dưới đây là đúng?
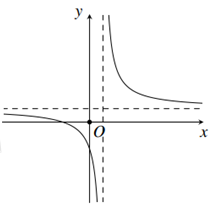
Từ đồ thị hàm số đã cho ta thấy :
+) Hàm số có 1 đường tiệm cận đứng là \(x = m > 0\) nên \(\dfrac{{ - d}}{c} > 0 \Leftrightarrow \dfrac{d}{c} < 0,\,\,\,d < 0 \Rightarrow c > 0\).
+) Hàm số có 1 đường tiệm cận ngang là \(y = n > 0\) nên \(\dfrac{a}{c} > 0,\,\,\,c > 0 \Rightarrow a > 0\).
+) Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên \(\dfrac{b}{d} < 0,\,\,\,d < 0 \Rightarrow b > 0\).
Vậy \(a > 0,\,\,b > 0,\,\,c > 0\).
Hàm số nào dưới đây có bảng biến thiên như hình vẽ
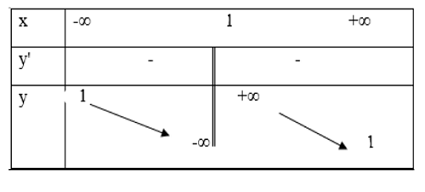
Quan sát BBT ta thấy:
- Đồ thị hàm số có TCĐ \(x = 1\) nên loại đáp án A.
- Đồ thị hàm số có \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } f(x) = 1 \Rightarrow \)TCN \(y = 1\) nên loại đáp án C.
- Hàm số nghịch biến trên TXĐ nên loại đáp án B (do đáp án B có \(y' = \dfrac{2}{{{{\left( {x - 1} \right)}^2}}} > 0\,\,\forall x \ne 1\)).
Bảng biến thiên sau đây là của hàm số nào?
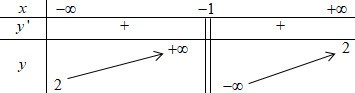
Dựa vào BBT ta có: \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} f\left( x \right) = - \infty ,\,\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} f\left( x \right) = + \infty \Rightarrow \) Đồ thị hàm số có TCĐ \(x = - 1\). Do đó loại phương án A, D.
Lại có: \(\mathop {\lim }\limits_{x \to \infty } y = 2\) nên đồ thị hàm số có TCN \(y = 2\), do đó loại đáp án B.
Hàm số nào dưới đây có tập xác định bằng \(\mathbb{R}\)?
Đáp án A: Hàm số xác định nếu \(x \ne 0\) nên loại.
Đáp án B: Hàm số xác định nếu \(x \ne - 1\) nên loại.
Đáp án C: Hàm số xác định nếu \({x^2} + 1 \ge 0\) luôn đúng nên C đúng.
Đáp án D: Hàm số xác định nếu \({x^2} - 1 \ne 0 \Leftrightarrow x \ne \pm 1\) nên loại.
Hàm số \(y = \dfrac{{3x - 6}}{{x - 2}}\) xác định khi:
Hàm số xác định khi \(x - 2 \ne 0 \Leftrightarrow x \ne 2\).
Hàm số nào dưới đây không có cực trị?
Dễ thấy hàm số \(y = \dfrac{{x - 2}}{{x + 1}}\) là hàm phân thức bậc nhất trên bậc nhất nên không có cực trị.
Ngoài ra, có thể kiểm tra được các cực trị của mỗi hàm số được cho ở ba đáp án B, C, D.

