Câu hỏi:
2 năm trước
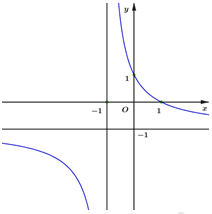
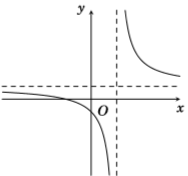
Cho hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có đồ thị là đường cong trong hình vẽ bên. Kết luận nào sau đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: b
Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có TCN \(y = \dfrac{a}{c}\), TCĐ \(x = - \dfrac{d}{c}\).
Dựa vào đồ thị hàm số ta thấy \(\dfrac{a}{c} > 0 \Leftrightarrow ac > 0\), \( - \dfrac{d}{c} > 0 \Leftrightarrow cd < 0\).
\( \Rightarrow ac.cd < 0 \Leftrightarrow ad.{c^2} < 0 \Leftrightarrow ad < 0\), do đó loại đáp án A và D.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên thay \(x = 0\) ta có \(\dfrac{b}{d} < 0 \Leftrightarrow bd < 0\).
\( \Rightarrow cd.bd > 0 \Leftrightarrow bc.{d^2} > 0 \Leftrightarrow bc > 0\), loại đáp án C.
Vậy \(ad < 0,\,\,bc > 0\).
Hướng dẫn giải:
- Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có TCN \(y = \dfrac{a}{c}\), TCĐ \(x = - \dfrac{d}{c}\).
- Dựa vào giao điểm của đồ thị hàm số với trục tung.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
