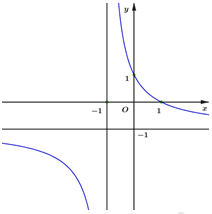
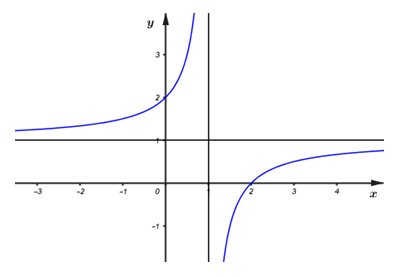
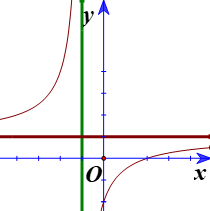
Hình vẽ dưới là đồ thị của hàm số \(y = \dfrac{{ax + b}}{{cx + d}}(ad - bc \ne \) . Mệnh đề nào sau đây là đúng?

Bước 1: Xác định giao điểm với trục hoành và đánh giá ab.

Từ đồ thị suy ra đồ thị hàm số đã cho cắt trục hoành tại điểm có hoành độ dương.

Mặt khác, từ \(y = \dfrac{{ax + b}}{{cx + d}}\) suy ra đồ thị hàm số đã cho cắt trục hoành tại điểm \(A\left( { - \dfrac{b}{a};0} \right)\).

Từ đồ thị hàm số suy ra \( - \dfrac{b}{a} > 0 \Rightarrow ab < 0\).

Bước 2: Từ các đường tiệm cận suy ra tích ad.

Từ hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) suy ra đồ thị có các đường tiệm cận ngang và đứng lần lượt là:

\( = \dfrac{a}{c};x =  - \dfrac{d}{c}\)

Từ đồ thị hàm số suy ra \(\left\{ {\begin{array}{*{20}{l}}{\dfrac{a}{c} > 0}\\{ - \dfrac{d}{c} < 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{ac > 0}\\{dc > 0}\end{array}} \right.} \right.\)

\( \Rightarrow ad{c^2} > 0 \Rightarrow ad > 0\).