Câu hỏi:
2 năm trước
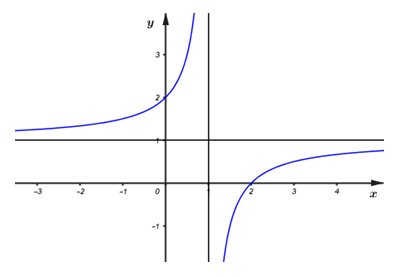
Hình sau là đồ thị của hàm số \(y = \dfrac{{ax + b}}{{x + c}}\) (với \(a,b,c \in \mathbb{R}\)).
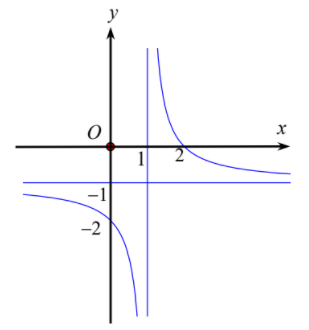
Khi đó \(ab - c\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
Bước 1: Tính giới hạn của hàm số tại vô cực để tính a, tìm đường tiệm cận đứng, từ đó tìm c
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = - 1 \Rightarrow \dfrac{a}{1} = - 1 \Rightarrow a = - 1\)
\(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty \Rightarrow c = - 1\)
Bước 2: Thay tọa độ điểm (0;-2) vào hàm số tìm b, tính ab-c.
Thay tọa độ của (0;-2) vào ta được:
\( - 2 = \dfrac{b}{c} \Rightarrow b = - 2c = 2\)
\( \Rightarrow ab - c = - 1\)
Hướng dẫn giải:
Bước 1: Tính giới hạn của hàm số tại vô cực để tính a, tìm đường tiệm cận đứng, từ đó tìm c
Bước 2: Thay tọa độ điểm (0;-2) vào hàm số tìm b, tính ab-c.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
