Trả lời bởi giáo viên
Đáp án đúng: d
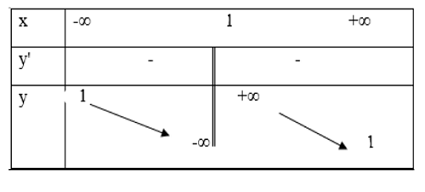
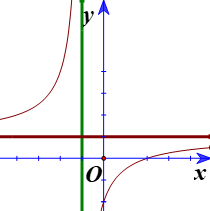
Quan sát BBT ta thấy:
- Đồ thị hàm số có TCĐ \(x = 1\) nên loại đáp án A.
- Đồ thị hàm số có \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } f(x) = 1 \Rightarrow \)TCN \(y = 1\) nên loại đáp án C.
- Hàm số nghịch biến trên TXĐ nên loại đáp án B (do đáp án B có \(y' = \dfrac{2}{{{{\left( {x - 1} \right)}^2}}} > 0\,\,\forall x \ne 1\)).
Hướng dẫn giải:
- Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\,\,\left( {ad \ne bc} \right)\) có TCN \(y = \dfrac{a}{c}\) và TCĐ \(x = - \dfrac{d}{c}\).
- Dựa vào tính đơn điệu của hàm số.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
