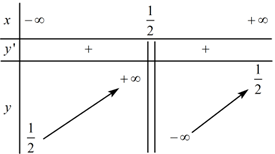
Cho hàm số \(y=\dfrac{ax+b}{cx+1}\) có bảng biến thiên:

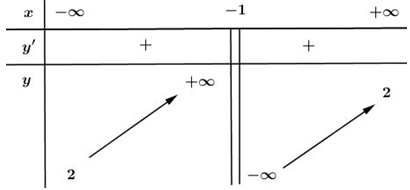
Xét các mệnh đề:

\(\begin{align}  & \left( 1 \right)\,\,\,\,\,c=1 \\  & \left( 2 \right)\,\,\,\,a=2 \\ \end{align}\)

(3) Hàm số đồng biến trên \(\left( -\infty ;-1 \right)\cup \left( -1;+\infty  \right).\)

(4) Nếu \(y'=\frac{1}{{{\left( x+1 \right)}^{2}}}\) thì \(b=1.\)

Tìm số mệnh đề đúng trong các mệnh đề trên.

TXĐ: \(D=R\backslash \left\{ -\frac{1}{c} \right\}.\)

Ta có: \(y'=\frac{a-bc}{{{\left( cx+1 \right)}^{2}}}.\)

Ta thấy đồ thị có TCĐ \(x=-1\Rightarrow -\frac{1}{c}=-1\Rightarrow c=1\Rightarrow \) Mệnh đề (1) đúng.

Đồ thị hàm số có TCN \(y=2\Rightarrow \frac{a}{c}=2\Leftrightarrow a=2c=2\Rightarrow \) Mệnh đề (2) đúng.

Theo BBT ta thấy hàm số đồng biến trên từng khoảng xác định của hàm số.

\(\Rightarrow y'>0\Leftrightarrow a-bc>0\) do \({{\left( cx+1 \right)}^{2}}>0\,\,\,\forall x\in D \)

\(\Rightarrow \) Hàm số đồng biến trên \(\left( -\infty ;\,\,-1 \right)\) và \(\left( -1;+\infty  \right)\Rightarrow \) Mệnh đề (3) sử dụng kí hiệu hợp nên sai.

Nếu \(y'=\frac{1}{{{\left( x+1 \right)}^{2}}}\Rightarrow \frac{a-bc}{{{\left( cx+1 \right)}^{2}}}=\frac{1}{{{\left( x+1 \right)}^{2}}}\)

\(\begin{align}  & \Leftrightarrow \frac{2-b}{{{\left( x+1 \right)}^{2}}}=\frac{1}{{{\left( x+1 \right)}^{2}}}\Leftrightarrow 2-b=1 \\  & \Leftrightarrow b=1. \\ \end{align}\)

\(\Rightarrow \) Mệnh đề (4) đúng.

Như vậy có 3 mệnh đề đúng.