Cho hàm số $y = \dfrac{{2x + 1}}{{x - 2}}$. Khẳng định nào dưới đây là đúng?

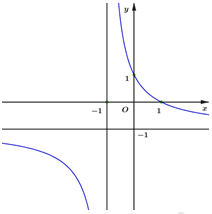
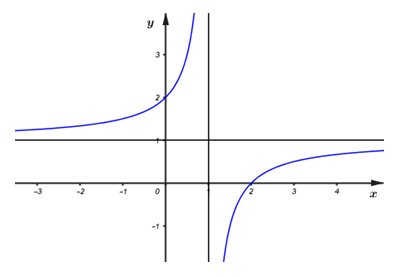
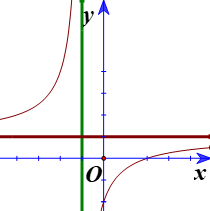
Xét hàm số $y = \dfrac{{2x + 1}}{{x - 2}}$:

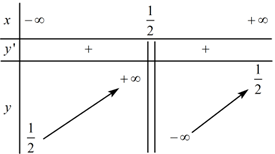
+) $\mathop {\lim }\limits_{x \to {2^ + }} {\mkern 1mu} \dfrac{{2x + 1}}{{x - 2}} =  + \infty ,{\mkern 1mu} {\mkern 1mu} \mathop {\lim }\limits_{x \to {2^ - }} {\mkern 1mu} \dfrac{{2x + 1}}{{x - 2}} =  - \infty  \Rightarrow $

Đồ thị hàm số có tiệm cận đứng là$x = 2$. Phương án A: đúng.

+) $y' =  - \dfrac{5}{{{{(x - 2)}^2}}} < 0,{\mkern 1mu} {\mkern 1mu} \forall x \ne 2 \Rightarrow $ Hàm số $y = \dfrac{{2x + 1}}{{x - 2}}$ không có cực trị và hàm số nghịch biến trên các khoảng $\left( { - \infty ;2} \right);{\mkern 1mu} {\mkern 1mu} \left( {2; + \infty {\rm{\;}}} \right)$. Phương án B và D: sai.

+) Ta có: $3 = \dfrac{{2.1 + 1}}{{1 - 2}}$ vô lí  $ \Rightarrow $Đồ thị hàm số không đi qua điểm$A(1;3)$. Phương án C: sai.