Câu hỏi:
2 năm trước
Cho $x$, $y$ là các số thực dương thỏa mãn \({5^{x + 2y}} + \dfrac{3}{{{3^{xy}}}} + x + 1 = \dfrac{{{5^{xy}}}}{5} + {3^{ - x - 2y}} + y(x - 2)\). Tìm giá trị nhỏ nhất của biểu thức \(T = x + y\).
Trả lời bởi giáo viên
Đáp án đúng: b
Theo đề ra ta có
\(\begin{array}{l}{5^{x + 2y}} + \dfrac{3}{{{3^{xy}}}} + x + 1 = \dfrac{{{5^{xy}}}}{5} + {3^{ - x - 2y}} + y(x - 2)\\ \Leftrightarrow {5^{x + 2y}} - \dfrac{1}{{{3^{x + 2y}}}} + x + 2y = {5^{xy - 1}} - \dfrac{1}{{{3^{xy - 1}}}} + xy - 1\end{array}\)
Xét \(f\left( t \right) = {5^t} - \dfrac{1}{{{3^t}}} + t\).\( \Rightarrow f'\left( t \right) = {5^t}\ln 5 + {3^{ - t}}\ln 3 + 1 > 0\)
\( \Rightarrow x + 2y = xy - 1 \Rightarrow y = \dfrac{{x + 1}}{{x - 2}}\).
Do \(y > 0,x > 0 \Rightarrow \dfrac{{x + 1}}{{x - 2}} > 0 \Rightarrow x > 2\)
Ta có: \(T = x + y = x + \dfrac{{x + 1}}{{x - 2}} = \dfrac{{{x^2} - x + 1}}{{x - 2}}\)
$T' = \dfrac{{{x^2} - 4x + 1}}{{{{\left( {x - 2} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2 + \sqrt 3 \in \left( {2; + \infty } \right)\\x = 2 - \sqrt 3 \notin \left( {2; + \infty } \right)\end{array} \right.$
Bảng biến thiên
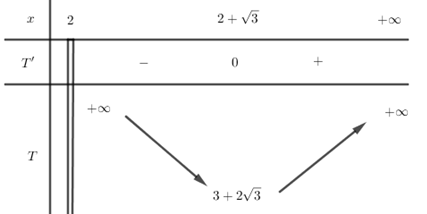
Từ bảng biến thiên ta thấy \({T_{\min }} = 3 + 2\sqrt 3 \) tại \(x = 2 + \sqrt 3 \).
Hướng dẫn giải:
- Biến đổi phương trình về dạng \(f\left( u \right) = f\left( v \right)\) với \(u,v\) là các biểu thức của \(x,y\)
- Xét hàm \(y = f\left( t \right)\) suy ra mối quan hệ của \(u,v\) dẫn đến \(x,y\)
- Tìm \(GTNN\) của \(T\) bằng phương pháp hàm số và kết luận.
