Cho $0 \le x;y \le 1$ thỏa mãn ${2017^{1 - x - y}} = \dfrac{{{x^2} + 2018}}{{{y^2} - 2y + 2019}}$. Gọi $M$, $m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(S = \left( {4{x^2} + 3y} \right)\left( {4{y^2} + 3x} \right) + 25xy\). Khi đó $M + m$ bằng bao nhiêu?

Ta có ${2017^{1 - x - y}} = \dfrac{{{x^2} + 2018}}{{{y^2} - 2y + 2019}}$ $ \Leftrightarrow $ $\dfrac{{{{2017}^{1 - y}}}}{{{{2017}^x}}} = \dfrac{{{x^2} + 2018}}{{{{\left( {1 - y} \right)}^2} + 2018}}$

 $ \Leftrightarrow {2017^{1 - y}}\left[ {{{\left( {1 - y} \right)}^2} + 2018} \right]$$ = {2017^x}\left( {{x^2} + 2018} \right)$

Xét hàm số $f\left( t \right) = {2017^t}\left( {{t^2} + 2018} \right)$, với $0 \le t \le 1$.

$ \Rightarrow $ $f'\left( t \right) = \left( {{t^2} + 2018} \right){.2017^t}.\ln 2017 + 2t{.2017^t}$ $ = {2017^t}\left[ {\left( {{t^2} + 2018} \right).\ln 2017 + 2t} \right] > 0, \forall x \in [0;1]$

$ \Rightarrow $ Hàm số $f\left( t \right)$ đồng biến trên $[0;1]$

$ \Rightarrow $ $1 - y = x$ $ \Leftrightarrow $ $y = 1 - x$

Theo giả thiết \(S = \left( {4{x^2} + 3y} \right)\left( {4{y^2} + 3x} \right) + 25xy\)

\(\begin{array}{l} = \left[ {4{x^2} + 3\left( {1 - x} \right)} \right].\left[ {4{{\left( {1 - x} \right)}^2} + 3x} \right] + 25x\left( {1 - x} \right)\\ = \left( {4{x^2} - 3x + 3} \right)\left( {4{x^2} - 5x + 4} \right) + 25x\left( {1 - x} \right)\\ = 16{x^4} - 20{x^3} + 16{x^2} - 12{x^3} + 15{x^2} - 12x + 12{x^2} - 15x + 12 + 25x - 25{x^2}\\ = 16{x^4} - 32{x^3} + 18{x^2} - 2x + 12\end{array}\)

Xét hàm số \(S\left( x \right) = 16{x^4} - 32{x^3} + 18{x^2} - 2x + 12\), với $0 \le x \le 1$.

$ \Rightarrow $ $S'\left( x \right) = 64{x^3} - 96{x^2} + 36x - 2$. Cho $S'\left( x \right) = 0$ $ \Leftrightarrow $ $\left[ \begin{array}{l}x = \dfrac{{2 \pm \sqrt 3 }}{4}\\x = \dfrac{1}{2}\end{array} \right.$

Bảng biến thiên

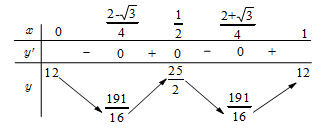
Từ bảng biến thiên, ta có $\left\{ \begin{array}{l}M = \mathop {\max }\limits_{\left[ {0;1} \right]} S\left( x \right) = \dfrac{{25}}{2}\\m = \mathop {\min }\limits_{\left[ {0;1} \right]} S\left( x \right) = \dfrac{{191}}{{16}}\end{array} \right.$.

Vậy $M + m = \dfrac{{25}}{2} + \dfrac{{191}}{{16}} = \dfrac{{391}}{{16}}$.