Trong không gian với hệ tọa độ ${\rm{Ox}}yz$, mặt phẳng \(\left( \alpha \right)\) chắn các trục $Ox,\,\,Oy,\,\,Oz$ lần lượt tại $A,\,\,B,\,\,C$ sao cho $H\left( {3;\,\, - 4;\,\,2} \right)$ là trực tâm của tam giác \(ABC\). Phương trình mặt phẳng \(\left( \alpha \right)\) là
Trả lời bởi giáo viên
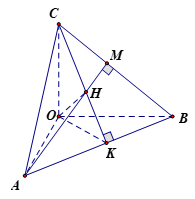
Gọi \(CK,\,\,AM\) là hai đường cao của tam giác \(ABC\).
Suy ra \(H = AM \cap CK\).
Ta có: $\left. \begin{array}{l}AB \bot \left( {OKC} \right) \Rightarrow AB \bot OH\\BC \bot \left( {AOM} \right) \Rightarrow BC \bot OH\end{array} \right\} \Rightarrow OH \bot \left( {ABC} \right)$
Mặt phẳng $\left( {ABC} \right)$đi qua điểm $H$ và nhận \(\overrightarrow {OH} \) làm một \(VTPT\)
Nên mặt phẳng $\left( {ABC} \right)$ có phương trình: \(3x - 4y + 2z - 29 = 0\).
Hướng dẫn giải:
Mặt phẳng cần tìm đi qua \(H\) và vuông góc với \(\overrightarrow {OH} \)

