Câu hỏi:
2 năm trước
Cho mặt cầu \(\left( S \right)\). Biết rằng khi cắt mặt cầu \(\left( S \right)\) bởi một mặt phẳng cách tâm một khoảng có độ dài là 3 thì được giao tuyến là đường tròn \(\left( T \right)\) có chu vi là \(12\pi\). Diện tích của mặt cầu \(\left( S \right)\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: a
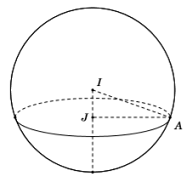
Gọi \(I,\,\,J\) theo thứ tự là tâm mặt cầu \(\left( S \right)\) và đường tròn \(\left( T \right)\), \(A\) là điểm bất kì thuộc đường tròn \(\left( T \right)\). Khi đó ta có \(IJ = 3\), \(2\pi .AJ = 12\pi \Leftrightarrow AJ = 6\).
Áp dụng định lí Pytago trong tam giác vuông \(AIJ\) ta có: \(AI = \sqrt {A{J^2} + I{J^2}} = \sqrt {{6^2} + {3^2}} = 3\sqrt 5 \).
\( \Rightarrow \) Bán kính của mặt cầu là \(R = 3\sqrt 5 \).
Vậy diện tích mặt cầu \(\left( S \right)\) là: \(S = 4\pi {R^2} = 4\pi .{\left( {3\sqrt 5 } \right)^2} = 180\pi .\)
Hướng dẫn giải:
- Tính bán kính của đường tròn giao tuyến \(\left( T \right)\), sử dụng công thức chu vi đường tròn có bán kính \(r\) là \(C = 2\pi r\)
- Sử dụng định lí Pytago tính bán kính mặt cầu \(\left( S \right)\): \(R = \sqrt {{r^2} + {d^2}} \) với \(d\) là khoảng cách từ tâm của mặt cầu \(\left( S \right)\) đến mặt phẳng chứa đường tròn \(\left( T \right)\).
- Diện tích mặt cầu bán kính \(R\) là: \(S = 4\pi {R^2}\).
