Trong không gian \(Oxyz\), cho điểm \(A\left( {2; - 3;4} \right)\), đường thẳng \(d:\,\,\dfrac{{x - 1}}{2} = \dfrac{{y + 2}}{1} = \dfrac{z}{2}\) và mặt cầu \(\left( S \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 20\). Mặt phẳng \(\left( P \right)\) chứa đường thẳng d thỏa mãn khoảng cách từ điểm \(A\) đến \(\left( P \right)\) lớn nhất. Mặt cầu \(\left( S \right)\) cắt \(\left( P \right)\) theo đường tròn có bán kính bằng :
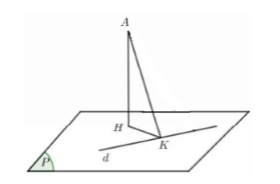
Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(A\) lên \(\left( P \right)\) và \(d\) ta có \(AH \le AK\), khi đó mặt phẳng \(\left( P \right)\) chứa đường thẳng d thỏa mãn khoảng cách từ điểm \(A\) đến \(\left( P \right)\) lớn nhất \( \Leftrightarrow \left( P \right)\) nhận \(\overrightarrow {AK} \) là 1 VTPT.
Gọi \(K\left( {1 + 2t; - 2 + t;2t} \right) \in d \Rightarrow \overrightarrow {AK} = \left( {2t - 1;t + 1;2t - 4} \right)\).
\(\overrightarrow {{u_d}} \left( {2;1;2} \right)\) là 1 VTCP của \(d\).
\(\begin{array}{l} \Rightarrow \overrightarrow {AK} .\overrightarrow {{u_d}} = 0 \Leftrightarrow 4t - 2 + t + 1 + 4t - 8 = 0 \Leftrightarrow 9t - 9 = 0 \Leftrightarrow t = 1\\ \Rightarrow K\left( {3; - 1;2} \right) \Rightarrow \overrightarrow {AK} = \left( {1;2; - 2} \right)\end{array}\)
\( \Rightarrow \left( P \right):\,\,x - 3 + 2\left( {y + 1} \right) - 2\left( {z - 2} \right) = 0 \Leftrightarrow x + 2y - 2z + 3 = 0\).
Mặt cầu \(\left( S \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 20\) có tâm \(I\left( {3;2; - 1} \right)\), bán kính \(R = \sqrt {20} = 2\sqrt 5 \).
Ta có: \(d = d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {3 + 2.2 - 2\left( { - 1} \right) + 3} \right|}}{{\sqrt {1 + 4 + 4} }} = \dfrac{{12}}{3} = 4\).
Gọi \(r\) là đường kính đường tròn giao tuyến của \(\left( P \right)\) và \(\left( S \right)\) ta có:
\({R^2} = {d^2} + {r^2} \Leftrightarrow r = \sqrt {{R^2} - {d^2}} = \sqrt {20 - 16} = 2\).
Cho mặt cầu \(\left( S \right)\) có đường kính 10 cm và mặt phẳng \(\left( P \right)\) cách tâm mặt cầu một khoảng 4 cm. Khẳng định nào sau đây sai?
Mặt cầu \(\left( S \right)\) có đường kính là 10cm bán kính \(R = 5cm\).
Mà khoảng cách từ tâm của mặt cầu và mặt phẳng \(\left( P \right)\) là \(d = 4cm < R\).
Do đó mặt phẳng \(\left( P \right)\) cắt \(\left( S \right)\) theo một đường tròn có bán kính \(r = \sqrt {{R^2} - {d^2}} = 3\,\,\left( {cm} \right)\).
Vậy trong 4 đáp án chỉ có đáp án C sai.
Cho hình cầu bán kính bằng \(2a\). Thể tích lớn nhất của khối trụ nội tiếp trong hình cầu đã cho là:
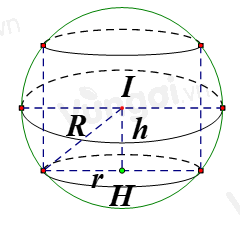
Gọi H là tâm mặt đáy. Đặt \(IH = h\)
Bán kính mặt đáy: \(r = \sqrt {{R^2} - {h^2}} \)
Thể tích khối trụ nội tiếp là: \(V = \pi {r^2}.2h = \pi \left( {{R^2} - {h^2}} \right).2h\)
\( \Rightarrow {V_{\max }} \Leftrightarrow h = \dfrac{R}{{\sqrt 3 }}\)\( \Rightarrow {V_{{\rm{max }}}} = \dfrac{{4{R^3}\sqrt 3 }}{9} = \dfrac{{4 \cdot {{(2a)}^3}\sqrt 3 }}{9} = \dfrac{{32{a^3}\sqrt 3 }}{9}\)

