Câu hỏi:
2 năm trước
Cho hình cầu bán kính bằng \(2a\). Thể tích lớn nhất của khối trụ nội tiếp trong hình cầu đã cho là:
Trả lời bởi giáo viên
Đáp án đúng: b
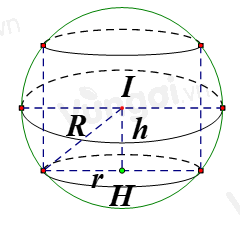
Gọi H là tâm mặt đáy. Đặt \(IH = h\)
Bán kính mặt đáy: \(r = \sqrt {{R^2} - {h^2}} \)
Thể tích khối trụ nội tiếp là: \(V = \pi {r^2}.2h = \pi \left( {{R^2} - {h^2}} \right).2h\)
\( \Rightarrow {V_{\max }} \Leftrightarrow h = \dfrac{R}{{\sqrt 3 }}\)\( \Rightarrow {V_{{\rm{max }}}} = \dfrac{{4{R^3}\sqrt 3 }}{9} = \dfrac{{4 \cdot {{(2a)}^3}\sqrt 3 }}{9} = \dfrac{{32{a^3}\sqrt 3 }}{9}\)
Hướng dẫn giải:
- Gọi H là tâm mặt đáy
- Tính bán kính mặt đáy
- \({V_{\max }} \Leftrightarrow h = \dfrac{R}{{\sqrt 3 }}\)

