Cho hình chóp đều $S . A B C$ cạnh đáy bằng $2 a$ và cạnh bên bằng $3 a$. Gọi \(M\) là điểm thay đổi trên cạnh \(AB,(P)\) qua \(M\) và song song với $S A, B C$ chia khối chóp $S . A B C$ thành hai phần. Biết thiết diện của hình chóp $S . A B C$ cắt bởi \((P)\) là hình thoi. Tính thể tích phần chứa đỉnh \(A\).

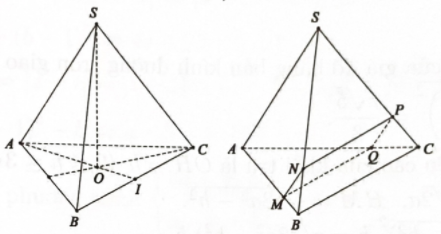
Bước 1: Gọi \(O\) là trọng tâm \(\Delta ABC,I\) là trung điểm $B C$. Chứng minh \(SO \bot (ABC)\)

Gọi \(O\) là trọng tâm \(\Delta ABC,I\) là trung điểm $B C$.

Gọi $N, P, Q$ lần lượt là giao điểm của \((P)\) với các cạnh $S B, S C, A C$.

 $S A B C$ là hình chóp đều nên \(SO \bot (ABC)\).

Bước 2: Tính \({V_{SABC}} = \dfrac{1}{3}SO \cdot {S_{ABC}}\)

Tam giác ABC đều có cạnh bằng \(2a\).

\( \Rightarrow AO = \dfrac{2}{3}AI = \dfrac{2}{3} \cdot \dfrac{{2a\sqrt 3 }}{2} = \dfrac{{2a\sqrt 3 }}{3}\)

Xét tam giác vuông $S O A$ có: \(SO = \sqrt {S{A^2} - A{O^2}}  = \dfrac{{a\sqrt {69} }}{3}\).

Ta có: \({V_{SABC}} = \dfrac{1}{3}SO \cdot {S_{ABC}}\)\( = \dfrac{1}{3} \cdot \dfrac{{a\sqrt {69} }}{3} \cdot \dfrac{{{{(2a)}^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt {23} }}{3}\).

Bước 3: Tính MN theo a.

MNPQ là hình thoi \( \Rightarrow MN = MQ = x\).

Ta có: \(\dfrac{{MN}}{{SA}} + \dfrac{{MQ}}{{BC}} = 1 \Leftrightarrow \dfrac{x}{{3a}} + \dfrac{x}{{2a}} = 1\)\( \Leftrightarrow x = \dfrac{{6a}}{5}\).

Bước 4: Đặt \(\dfrac{{AM}}{{AB}} = t\). Tính \({V_{SAMNPQ}}\).

Đặt \(\dfrac{{AM}}{{AB}} = t\).

=> \(t = \dfrac{{AM}}{{AB}} = \dfrac{{MQ}}{{BC}} = \dfrac{{\dfrac{{6a}}{5}}}{{2a}} = \dfrac{3}{5}\).

Ta có công thức tính nhanh \(\dfrac{{{V_{SAMNPQ}}}}{{{V_{S.ABC}}}} = {t^2}(3 - 2t)\).

\( \Rightarrow \dfrac{{{V_{SAMNPQ}}}}{{{V_{S.ABC}}}} = {t^2}(3 - 2t) = \dfrac{{81}}{{125}}\)\( \Rightarrow {V_{SAMNPQ}} = \dfrac{{81}}{{125}}{V_{S.ABC}} = \dfrac{{27\sqrt {23} {a^3}}}{{125}}\)