Câu hỏi:
2 năm trước
Cho hình chóp tứ giác đều \(S.ABCD\) có chiều cao bằng \(h\), góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {ABCD} \right)\) bằng \(\alpha \). Tính thể tích của khối chóp \(S.ABCD\) theo \(h\) và \(\alpha \).
Trả lời bởi giáo viên
Đáp án đúng: b
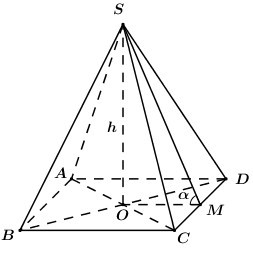
+ Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).
+ Gọi \(M\) là trung điểm của \(CD\) ta có: \(\left\{ \begin{array}{l}CD \bot OM\\CD \bot SO\end{array} \right. \Rightarrow CD \bot \left( {SOM} \right) \Rightarrow CD \bot SM\).
+ \(\left\{ \begin{array}{l}\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\SM \subset \left( {SCD} \right),\,\,SM \bot CD\\OM \subset \left( {ABCD} \right),\,\,OM \bot CD\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle \left( {SM;OM} \right) = \angle SMO = \alpha \).
+ \(\Delta SOM\): \(OM = SO.\cot \alpha = \dfrac{h}{{\tan \alpha }}\) \( \Rightarrow AD = 2OM = \dfrac{{2h}}{{\tan \alpha }}\) \( \Rightarrow {S_{ABCD}} = \dfrac{{4{h^2}}}{{{{\tan }^2}\alpha }}\).
+ \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.h.\dfrac{{4{h^2}}}{{{{\tan }^2}\alpha }} = \dfrac{{4{h^3}}}{{3{{\tan }^2}\alpha }}\).
Hướng dẫn giải:
- Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).
- Gọi \(M\) là trung điểm của \(CD\), chứng minh \(\angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle \left( {SM;OM} \right)\).
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính \(OM\) theo \(h\) và \(\alpha \), từ đó tính \({S_{ABCD}}\) theo \(h\) và \(\alpha \).
- Tính thể tích \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}\).
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
