Câu hỏi:
2 năm trước
Cho khối chóp đều $S . A B C D$ có \(AB = 2a\) và thể tích bằng \(\dfrac{{4\sqrt 3 }}{3}{a^3}\). Côsin góc giữa hai mặt phẳng \((SAB)\) và \((SCD)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: b
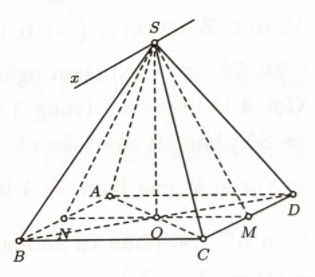
Bước 1: Gọi \(O\) là tâm hình vuông $A B C D$. Tính SO.
Gọi \(O\) là tâm hình vuông $A B C D$.
Ta có \({S_{ABCD}} = 4{a^2};{V_{S.ABCD}} = \dfrac{1}{3}{S_{ABCD}} \cdot SO\) \( \Rightarrow SO = a\sqrt 3 \).
Mặt khác \(AB//CD\)\( \Rightarrow (SAB) \cap (SCD) = Sx//AB//CD.\)
Bước 2: Gọi $M, N$ lần lượt là trung điểm của $C D$ và $A B$.
Gọi $M, N$ lần lượt là trung điểm của $C D$ và $A B$. Ta có:
\(SN \bot AB \Rightarrow SN \bot Sx\)
\(SM \bot CD\)\( \Rightarrow SM \bot Sx\).
\( \Rightarrow ((SAB),(SCD)) = (SM,SN)\)\( = \widehat {MSN} = 2\widehat {MSO}.\)
Ta có
\(\tan \widehat {MSO} = \dfrac{{OM}}{{SO}} = \dfrac{a}{{a\sqrt 3 }} = \dfrac{1}{{\sqrt 3 }}\)\( \Rightarrow \widehat {MSO} = {30^0 } \Rightarrow \widehat {MSN} = {60^0}\)\( \Rightarrow \cos \widehat {MSN} = \dfrac{1}{2}\)
Hướng dẫn giải:
Bước 1: Gọi \(O\) là tâm hình vuông $A B C D$. Tính SO.
Chứng minh \((SAB) \cap (SCD) = Sx//AB//CD\)
Bước 2: Gọi $M, N$ lần lượt là trung điểm của $C D$ và $A B$.
Tính cosin góc giữa hai mặt phẳng \((SAB)\) và \((SCD)\)
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
