Cho hình chóp đều \(S.ABC\), góc giữa mặt bên và mặt phẳng đáy \(\left( {ABC} \right)\) bằng \({60^0}\), khoảng cách giữa hai đường thẳng \(SA\) và \(BC\) bằng \(\dfrac{{3a}}{{2\sqrt 7 }}\). Thể tích của khối chóp \(S.ABC\) theo \(a\) bằng:

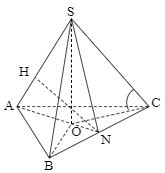
+ Gọi \(O\) là tâm tam giác đều \(ABC\) \( \Rightarrow SO \bot \left( {ABC} \right)\).

+ Gọi \(N\) là trung điểm \(BC\) ta có: \(\left\{ \begin{array}{l}BC \bot AN\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SAN} \right) \Rightarrow BC \bot SN\).

+ \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\SN \subset \left( {SBC} \right),\,\,SN \bot BC\\AN \subset \left( {ABC} \right),\,\,AN \bot BC\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SN;AN} \right) = \angle SNA = {60^0}\).

+ Trong \(\left( {SAM} \right)\) kẻ \(NH \bot SA\,\,\left( {H \in SA} \right)\) \( \Rightarrow NH \bot BC\) \( \Rightarrow d\left( {SA;BC} \right) = NH = \dfrac{{3a}}{{2\sqrt 7 }}\).

+ Đặt \(ON = x \Rightarrow AN = 3x,\,\,OA = 2x\).

+  \(\Delta SON:\,\,SO = ON.\tan {60^0} = x\sqrt 3 \), \(SA = \sqrt {S{O^2} + O{A^2}}  = \sqrt {3{x^2} + 4{x^2}}  = x\sqrt 7 \).

+ \(\Delta SAN:\,\,{S_{\Delta SAN}} = \dfrac{1}{2}SO.AN = \dfrac{1}{2}NH.SA\)

\(\begin{array}{l} \Rightarrow SO.AN = NH.SA\\ \Rightarrow x\sqrt 3 .3x = \dfrac{{3a}}{{2\sqrt 7 }}.x\sqrt 7 \\ \Leftrightarrow x = \dfrac{a}{{2\sqrt 3 }}\end{array}\)

\(\begin{array}{l} \Rightarrow AM = 3a = \dfrac{{a\sqrt 3 }}{2} = \dfrac{{AB\sqrt 3 }}{2} \Rightarrow AB = a\\ \Rightarrow {S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\end{array}\)

Và \(SO = x\sqrt 3  = \dfrac{a}{2}\).

Vậy \({V_{S.ABC}} = \dfrac{1}{3}SO.{S_{\Delta ABC}} = \dfrac{1}{3}.\dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{24}}\).