Câu hỏi:
2 năm trước
Cho hình chóp S.ABCD đáy là hình chữ nhật, SA vuông góc với đáy, AB=a,AD=2a. Góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABC bằng:
Trả lời bởi giáo viên
Đáp án đúng: c
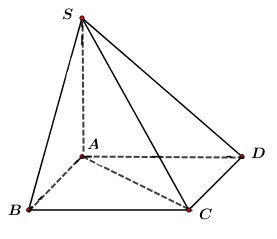
Ta có: SA⊥(ABCD) ⇒AB là hình chiếu của SB trên (ABCD)
⇒∠(SB,(ABCD))=∠(SB,AB)=∠SBA=450
⇒ΔSAB vuông cân tại A⇒SA=AB=a.
⇒VS.ABCD=13SA.SABC=13SA.12SABCD =13.a.12.a.2a=2a36.
Hướng dẫn giải:
Thể tích của khối chóp có diện tích đáy S và chiều cao h là: V=13Sh.

