Cho hình chóp \(S.ABCD\) đáy là hình chữ nhật, \(SA\) vuông góc với đáy, \(AB = a,\,\,AD = 2a.\) Góc giữa \(SB\) và đáy bằng \({45^0}.\) Thể tích khối chóp \(S.ABC\) bằng:
Trả lời bởi giáo viên
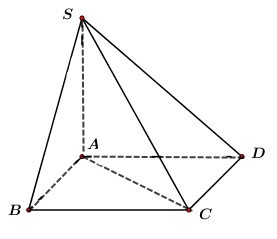
Ta có: \(SA \bot \left( {ABCD} \right)\) \( \Rightarrow AB\) là hình chiếu của \(SB\) trên \(\left( {ABCD} \right)\)
\( \Rightarrow \angle \left( {SB,\,\,\left( {ABCD} \right)} \right) = \angle \left( {SB,\,\,AB} \right) = \angle SBA = {45^0}\)
\( \Rightarrow \Delta SAB\) vuông cân tại \(A \Rightarrow SA = AB = a.\)
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}SA.\dfrac{1}{2}{S_{ABCD}}\) \( = \dfrac{1}{3}.a.\dfrac{1}{2}.a.2a = \dfrac{{2{a^3}}}{3}.\)
Hướng dẫn giải:
Thể tích của khối chóp có diện tích đáy \(S\) và chiều cao \(h\) là: \(V = \dfrac{1}{3}Sh.\)

