Khái niệm về thể tích của khối đa diện (thể tích khối chóp)

Thể tích khối tứ diện \(ABCD\) đã cho là: \(V = \frac{1}{6}AB.AC.AD = \frac{1}{6}.2a.3a.4a = 4{a^3}.\)

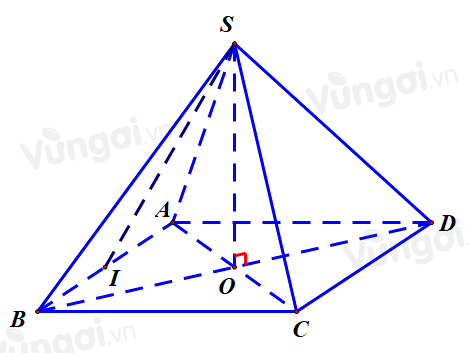
Gọi \(O\) là tâm hình vuông suy ra \(SO \bot (ABCD)\)

Ta có \((SAB) \cap (SCD) = Sx//AB//CD\)

Gọi \(I\) là trung điểm của $A B$

=> \(SI \bot AB \Rightarrow SI \bot Sx\)

\( \Rightarrow SI \bot (SCD) \Rightarrow SI \bot SD\)

\(AC = 4a \Rightarrow AD = 2\sqrt 2 a \Rightarrow DI = a\sqrt {10} \)

Đặt \(SD = x \Rightarrow SI = \sqrt {{x^2} - 2{a^2}} \).

Ta có hệ thức \({x^2} - 2{a^2} + {x^2} = 10{a^2}\) \( \Rightarrow {x^2} = 6{a^2} \Rightarrow x = a\sqrt 6 \)

Từ đó ta tính được \(SO = a\sqrt 2 \).

Vậy \({V_{S.ABCD}} = \dfrac{1}{3} \cdot a\sqrt 2  \cdot {(2\sqrt 2 a)^2} = \dfrac{{8\sqrt 2 }}{3}{a^3}\).

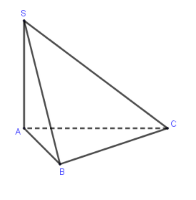
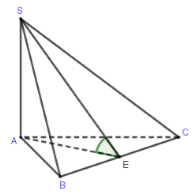
Gọi \(E\) là trung điểm của \(BC\) \( \Rightarrow \left\{ \begin{array}{l}AE \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAE} \right) \Rightarrow BC \bot SE\)

Ta có: \(\left\{ \begin{array}{l}AE \bot BC\\SE \bot BC\\\left( {ABC} \right) \cap \left( {SBC} \right) = BC\end{array} \right. \Rightarrow \angle \left( {\left( {ABC} \right);\left( {SBC} \right)} \right) = \angle SEA = {45^0}.\)

\( \Rightarrow \Delta SAE\) vuông cân tại \(A \Rightarrow SA = AE\).

Tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 2a\),

\(AE\) là tia phân giác của \(\widehat A\) \( \Rightarrow \widehat {BAE} = {60^0}\).

Tam giác vuông \(AEB\) có \(\widehat {BAE} = {60^0},BE = \dfrac{1}{2}BC = a \Rightarrow AE = \dfrac{{BE}}{{\tan {{60}^0}}} = \dfrac{{BE}}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{3} = SA\).

\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.SA.\dfrac{1}{2}AE.BC = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{3}.\dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{3}.2a = \dfrac{{{a^3}}}{9}\).

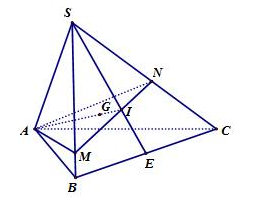
Đặt \(\dfrac{{SM}}{{SB}} = a;\,\dfrac{{SN}}{{SC}} = b\,\,\left( {0 < a;b < 1} \right)\)

Lấy \(E\) là trung điểm \(BC\).

Trong \(\left( {SAE} \right)\), kéo dài \(AG\) cắt \(SE\) tại \(I\). Khi đó \(I \in MN\) và \(I\) là trọng tâm tam giác \(SBC.\)

Khi đó trong tam giác \(SBC\) ta luôn có \(\dfrac{{SB}}{{SM}} + \dfrac{{SC}}{{SN}} = 3\) (tính chất đã được chứng minh ở trên)

Lại có \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}} = ab\)

Ta có \(\dfrac{{SB}}{{SM}} + \dfrac{{SC}}{{SN}} = 3\) \( \Leftrightarrow \dfrac{1}{a} + \dfrac{1}{b} = 3.\)

Xét \(\dfrac{1}{a} + \dfrac{1}{b}\mathop  \ge \limits^{Cô  - si} \dfrac{2}{{\sqrt {ab} }} \Leftrightarrow \sqrt {ab}  \ge \dfrac{2}{{\dfrac{1}{a} + \dfrac{1}{b}}} = \dfrac{2}{3} \Leftrightarrow ab \ge \dfrac{4}{9}\)

Dấu = xảy ra khi \(a = b = \dfrac{2}{3}\) .

Từ đó \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = ab \ge \dfrac{4}{9}\)  hay tỉ số \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}}\)  nhỏ nhất là bằng \(\dfrac{4}{9}.\)

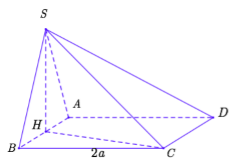
Gọi \(H\) là trung điểm của \(AB \Rightarrow SH \bot AB\) (do \(\Delta SAB\) cân tại \(S\))

Ta có \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\SH \bot AB;\,\,\,SH \subset \left( {SAB} \right)\end{array} \right. \Rightarrow SH \bot \left( {ABCD} \right)\)

Hay \(H\) là hình chiếu của \(S\) lên mặt phẳng \(\left( {ABCD} \right) \Rightarrow CH\) là hình chiều của \(SC\) lên mặt phẳng \(\left( {ABCD} \right)\)

Do đó góc giữa \(SC\) và mặt đáy là góc \(SCH.\)

Ta có \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} \Leftrightarrow \dfrac{{4{a^3}}}{3} = \dfrac{1}{3}SH.4{a^2} \Leftrightarrow SH = a\).

Xét tam giác \(BHC\) vuông tại \(B\), theo định lý Pytago ta có \(HC = \sqrt {B{H^2} + B{C^2}}  = \sqrt {{a^2} + {{\left( {2a} \right)}^2}}  = a\sqrt 5 \)

Xét tam giác \(SHC\) vuông tại \(H\) có \(\tan \angle SCH = \dfrac{{SH}}{{HC}} = \dfrac{a}{{a\sqrt 5 }} = \dfrac{{\sqrt 5 }}{5}\).

Ta có: \(V = \dfrac{1}{3}.B.h = \dfrac{8}{3}{a^3}\)

\({V_{chop}} = \dfrac{1}{3}{S_{day}} \times h = \dfrac{1}{3}.5{a^2}.a = \dfrac{5}{3}{a^3}\).

Ta có: \(V = \dfrac{1}{3}.B.h = \dfrac{1}{3}3{a^2}.a = {a^3}\)

Với bài toán, khối chóp tứ giác có cạnh bằng \(2a\) nên \(V = \dfrac{{{{\left( {2a} \right)}^3}\sqrt 2 }}{6} = \dfrac{{4\sqrt 2 {a^3}}}{3}.\)

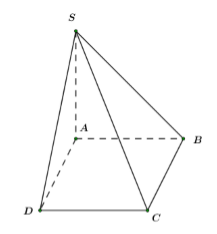
Ta có thể tích của khối chóp đã cho là:

\({V_{SABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.a.{a^2} = \dfrac{{{a^3}}}{3}.\)

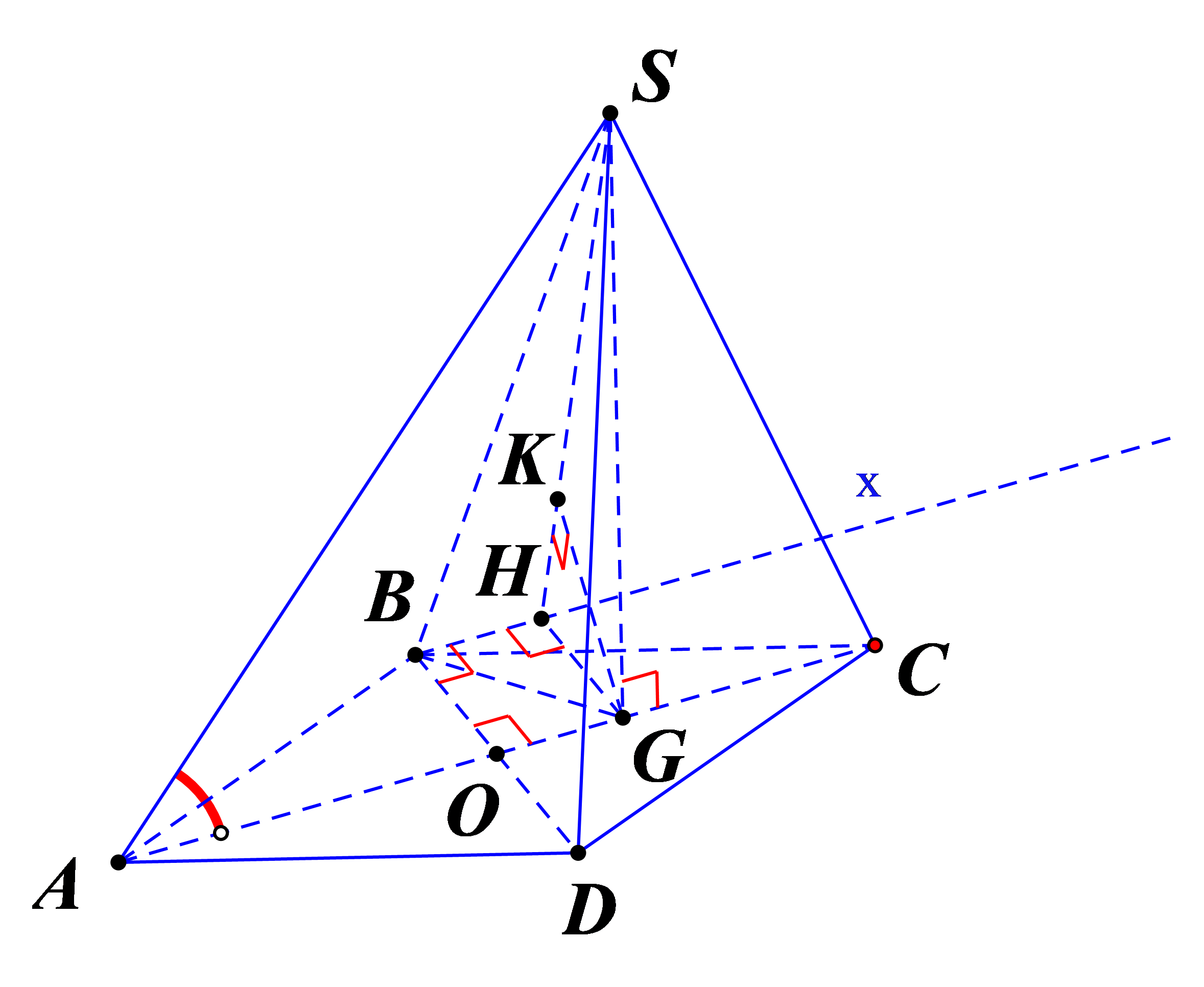
Kẻ Bx song song với AC.

Kẻ GH vuông góc với Bx, GK vuông góc với SH

Bước 1: Chứng minh \(GK \bot \left( {SBH} \right)\)

Ta có:

\(\begin{array}{l}\left. \begin{array}{l}GH \bot BH\\BH \bot SG\end{array} \right\} \Rightarrow BH \bot \left( {SGH} \right)\\\left. \begin{array}{l} \Rightarrow BH \bot GK\\GK \bot SH\end{array} \right\} \Rightarrow GK \bot \left( {SHB} \right)\end{array}\)

Bước 2: Chứng minh \(d\left( {AC,SB} \right) = GK\)

Ta có BH//AC  \( \Rightarrow AC//\left( {SHB} \right)\)

Mà \(SB \subset \left( {SHB} \right)\)

\( =  > d\left( {SB,AC} \right)\)\( = d\left( {AC,\left( {SHB} \right)} \right)\)\( = d\left( {G,\left( {SHB} \right)} \right) = GK\)

Bước 3: Tính GK

Dễ thấy tứ giác OBHG là hình chữ nhật

=> \(HG = OB = \dfrac{a}{2}\)

Áp dụng hệ thức lượng trong tam giác vuông SGH ta có:

\(\dfrac{1}{{G{K^2}}} = \dfrac{1}{{S{G^2}}} + \dfrac{1}{{G{H^2}}}\)\( = \dfrac{1}{{4{a^2}}} + \dfrac{4}{{{a^2}}} = \dfrac{{17}}{{4{a^2}}}\)

\( \Rightarrow GK = \dfrac{{2\sqrt {17} a}}{{17}}\)

Vậy \(d\left( {SB,AC} \right) = \dfrac{{2a\sqrt {17} }}{{17}}\)

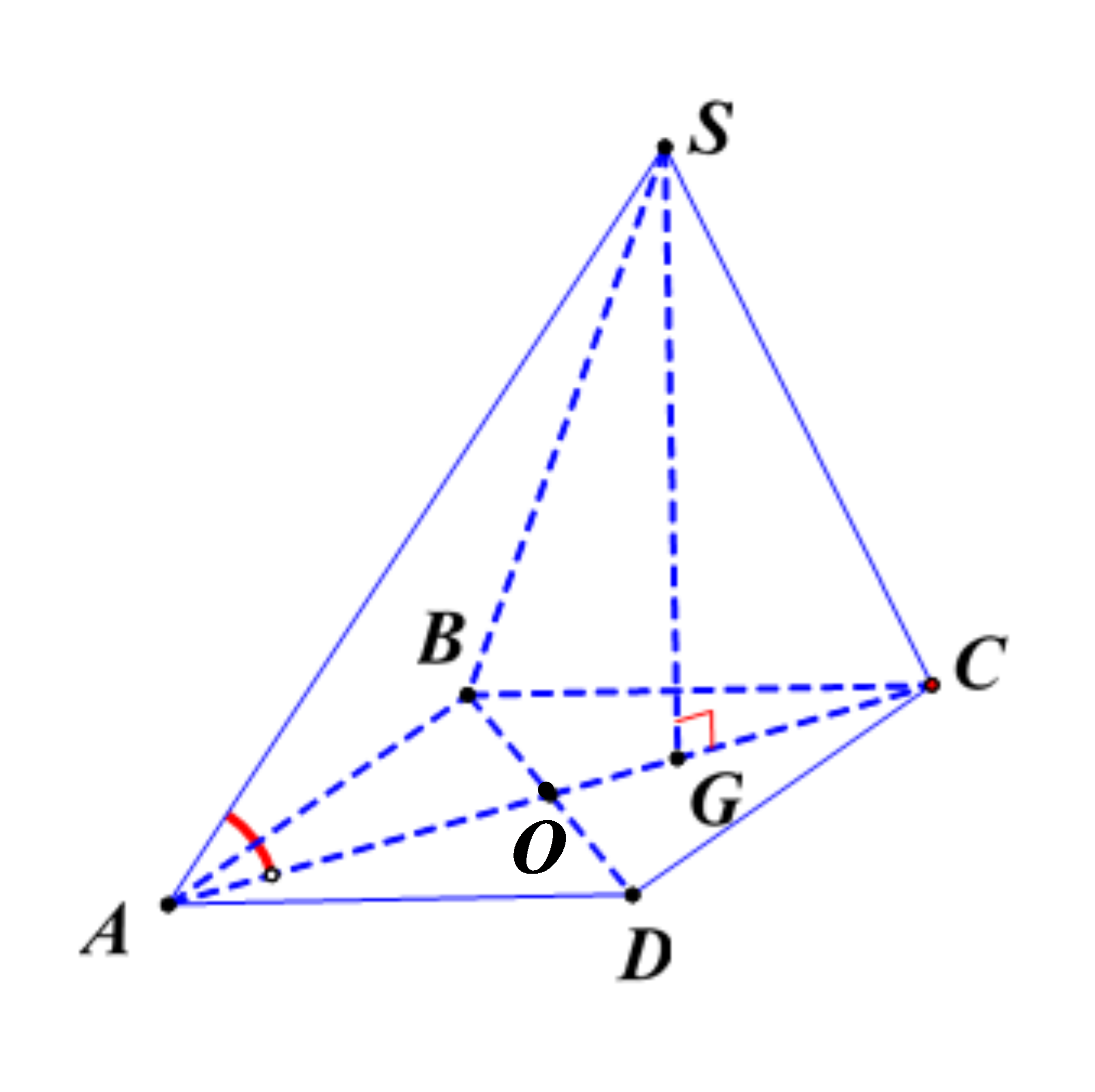
Bước 1: Tính AG.

Gọi O là giao điểm của AC và BD.

ABCD là hình thoi cạnh a nên BC=CD=a

\(\widehat {BAD} = \widehat {BCD} = {60^0}\)

=> Tam giác BCD là tam giác đều

=> \(CG = \dfrac{2}{3}.CO = \dfrac{2}{3}.\dfrac{{\sqrt 3 }}{2}BC = \dfrac{{\sqrt 3 }}{3}a\)

=> \(AG = 2CG = \dfrac{{2\sqrt 3 }}{3}a\)

Bước 2: Xác định góc giữa SA và đáy trên hình.

Do SG vuông góc với (ABCD) nên góc giữa SA và đáy bằng góc giữa SA và hình chiếu của nó trên (ABCD) tức là góc giữa SA và GA.

=> \(\widehat {SAG} = {60^0}\)

Bước 3: Tính SG

Tam giác vuông SAG có \(\widehat {SAG} = {60^0}\) nên \(SG = AG\sqrt 3  = \dfrac{{2\sqrt 3 }}{3}a.\sqrt 3  = 2a\)

Bước 4: Tính thể tích S.ABCD.

Ta có \(AC = 3CG = 3.\dfrac{{\sqrt 3 }}{3}a = a\sqrt 3 \)

Diện tích hình thoi ABCD là: \(S = \dfrac{1}{2}.AC.BD = \dfrac{1}{2}.a\sqrt 3 .a = \dfrac{{{a^2}\sqrt 3 }}{2}\)

Thể tích S.ABCD: \(V = \dfrac{1}{3}SG.{S_{ABCD}} = \dfrac{1}{3}.2a.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{3}\)

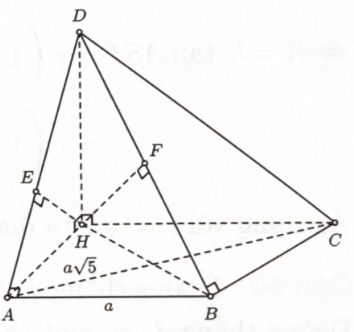
Bước 1: Kẻ \(DH \bot (ABC)\).Chứng minh \(BA \bot AH\) và \(BC \bot BH\)

Kẻ \(DH \bot (ABC)\).

Ta có \(\left\{ {\begin{array}{*{20}{l}}{BA \bot DA}\\{BA \bot DH}\end{array} \Rightarrow BA \bot (DAH)} \right.\)\( \Rightarrow BA \bot AH\).

Tương tự \(\left\{ {\begin{array}{*{20}{l}}{BC \bot DB}\\{BC \bot DH}\end{array} \Rightarrow BC \bot DBH} \right.\)\( \Rightarrow BC \bot BH\).

Bước 2: Tính \({S_{\Delta ABC}}\)

Tam giác AHB có \(AB = a,\widehat {ABH} = {45^0}\)

\( \Rightarrow \Delta HAB\) vuông cân tại \(A \Rightarrow AH = AB = a\).

Áp dụng định lý cosin, ta có \(BC = a\sqrt 2 \).

Vậy \({S_{\Delta ABC}} = \dfrac{1}{2} \cdot BA \cdot BC \cdot \sin \widehat {CBA}\)\( = \dfrac{1}{2} \cdot a \cdot a\sqrt 2  \cdot \dfrac{{\sqrt 2 }}{2} = \dfrac{{{a^2}}}{2}\).

Bước 3: Kẻ \(\left\{ {\begin{array}{*{20}{l}}{HE \bot DA}\\{HF \bot DB}\end{array}} \right.\). Đặt \(DH = x\). Tính HD và thể tích ABCD.

Kẻ \(\left\{ {\begin{array}{*{20}{l}}{HE \bot DA}\\{HF \bot DB}\end{array}} \right.\)

\( \Rightarrow HE \bot (DAB)\) và \(HF \bot (DBC)\).

Suy ra \((\widehat {(DBA),(DBC)}) = \widehat {(HE,HF)} = \widehat {EHF}\) và tam giác HEF vuông tại \(E\).

Đặt \(DH = x\), khi đó \(HE = \dfrac{{ax}}{{\sqrt {{a^2} + {x^2}} }},HF = \dfrac{{xa\sqrt 2 }}{{\sqrt {2{a^2} + {x^2}} }}\).

Suy ra \(\cos \widehat {EHF} = \dfrac{{HE}}{{HF}} = \sqrt {\dfrac{3}{4}} \)\( = \dfrac{{\sqrt {{x^2} + 2{a^2}} }}{{\sqrt {2{x^2} + 2{a^2}} }} \Rightarrow x = a\).

Vậy \({V_{ABCD}} = \dfrac{1}{3}.DH.{S_{\Delta ABC}} = \dfrac{{{a^3}}}{6}\).

Thể tích khối chóp là: \(V = \dfrac{1}{3}.18.7 = 42\).

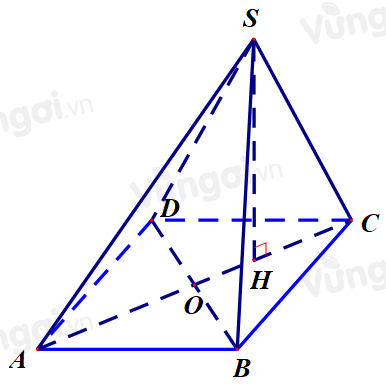
Bước 1: Gọi \(O\) là giao điểm của AC và BD. Chứng minh tam giác SAC vuông tại S.

Gọi \(O\) là giao điểm của AC và BD .

Ta có \(\Delta BAD = \Delta BSD = \Delta BCD\) nên \(AO = SO = CO\)

\( \Rightarrow SO = \dfrac{1}{2}AC\) \( \Rightarrow \Delta SAC\) vuông tại \(S\).

Bước 2: Biểu diễn AC, OD, BD theo x.

Do đó, \(AC = \sqrt {S{A^2} + S{C^2}}  = \sqrt {{x^2} + 4} \)

\( \Rightarrow OD = \sqrt {A{D^2} - A{O^2}}  = \sqrt {4 - \dfrac{{4 + {x^2}}}{4}}  = \dfrac{{\sqrt {12 - {x^2}} }}{2}\)

\( \Rightarrow BD = \sqrt {12 - {x^2}} ,0 < x < 2\sqrt 3 .\)

Bước 3: Trong \(\Delta SAC\) hạ \(SH \bot AC\). Chứng minh \(SH \bot \left( {ABCD} \right)\)

Ta thấy \(\left\{ {\begin{array}{*{20}{l}}{BD \bot AC}\\{BD \bot SO}\end{array} \Rightarrow BD \bot (SAC)} \right.\).

Trong \(\Delta SAC\) hạ \(SH \bot AC\).

Khi đó, \(\left\{ {\begin{array}{*{20}{l}}{SH \bot AC}\\{SH \bot BD}\end{array} \Rightarrow SH \bot (ABCD)} \right.\).

Bước 4: Lập phương trình dựa vào hệ thức lượng trong tam giác vuông SAC, tìm x.

Xét tam giác vuông SAC có \(\dfrac{1}{{S{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{S{C^2}}}\)

\( \Rightarrow SH = \dfrac{{SA.SC}}{{\sqrt {S{A^2} + S{C^2}} }} = \dfrac{{2x}}{{\sqrt {4 + {x^2}} }}\)

\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3} \cdot \dfrac{1}{2}\sqrt {{x^2} + 4}  \cdot \sqrt {12 - {x^2}}  \cdot \dfrac{{2x}}{{\sqrt {{x^2} + 4} }}\)

\( = \dfrac{1}{3}x.\sqrt {12 - {x^2}}  \le \dfrac{1}{3}\dfrac{{{x^2} + 12 - {x^2}}}{2} = 2\)

Dấu "=" xảy ra khi và chỉ khi \({x^2} = 12 - {x^2} \Rightarrow x = \sqrt 6 \).

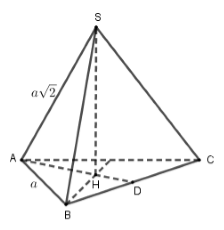
Đáy hình chóp là tam giác đều cạnh \(a\) nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\).

Có \(AD = \dfrac{{a\sqrt 3 }}{2} \Rightarrow AH = \dfrac{2}{3}AD = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).

Tam giác \(SAH\) vuông tại \(H\) có \(SA = a\sqrt 2 ,AH = \dfrac{{a\sqrt 3 }}{3} \Rightarrow SH = \sqrt {S{A^2} - A{H^2}}  = \dfrac{{a\sqrt {15} }}{3}\).

Thể tích \(V = \dfrac{1}{3}{S_{ABC}}.SH = \dfrac{1}{3}.\dfrac{{{a^2}\sqrt 3 }}{4}.\dfrac{{a\sqrt {15} }}{3} = \dfrac{{{a^3}\sqrt 5 }}{{12}}\).

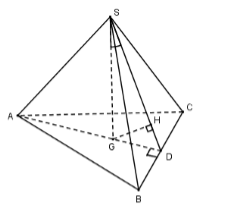
Vì chóp S.ABC đều nên \(SG \bot \left( {ABC} \right)\)

Gọi D là trung điểm của BC ta có: \(\left. \begin{array}{l}BC \bot SG\,\,\left( {SG \bot \left( {ABC} \right)} \right)\\BC \bot AD\end{array} \right\} \Rightarrow BC \bot \left( {SAD} \right)\)

Trong \(\left( {SAD} \right)\) kẻ \(GH \bot SD\,\,\left( 1 \right)\) ta có:\(BC \bot \left( {SAD} \right) \Rightarrow GH \bot BC\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra SH  là hình chiếu vuông góc của SG trên (SBC)

\( \Rightarrow \widehat {\left( {SG;\left( {SBC} \right)} \right)} = \widehat {\left( {SG;SH} \right)} = \widehat {GSH} = {30^0}\)

Vì tam giác ABC đều nên \(AD = \dfrac{{a\sqrt 3 }}{2} \Rightarrow GD = \dfrac{1}{3}AD = \dfrac{1}{3}\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}\)

\(SG \bot \left( {ABC} \right) \Rightarrow SG \bot GD \Rightarrow \Delta SGD\) vuông tại G\( \Rightarrow SG = GD.\cot 30 = \dfrac{{a\sqrt 3 }}{6}.\sqrt 3  = \dfrac{a}{2}\)

\({S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SG.{S_{\Delta ABC}} = \dfrac{1}{3}.\dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{24}}\)

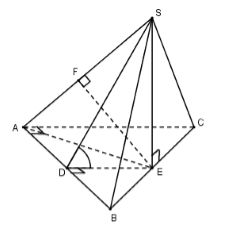
Gọi E là trung điểm của BC

Vì tam giác ABC vuông cân tại A nên E là tâm đường tròn ngoại tiếp tam giác ABC

\( \Rightarrow SE \bot \left( {ABC} \right)\)   

Gọi D là trung điểm của AB ta có DE là đường trung bình của tam giác ABC nên \(DE//AC \Rightarrow DE \bot AB\)

Ta có: \(\left. \begin{array}{l}DE \bot AB\\SE \bot AB\,\,\left( {SE \bot \left( {ABC} \right)} \right)\end{array} \right\} \Rightarrow AB \bot \left( {SDE} \right) \Rightarrow AB \bot SD\)

$\left. \begin{array}{l}\left( {SAB} \right) \cap \left( {ABC} \right) = AB\\\left( {SAB} \right) \supset SD \bot AB\\\left( {ABC} \right) \supset DE \bot AB\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SD;DE} \right)} = \widehat {SDE} = {60^0}$

(Vì \(SE \bot \left( {ABC} \right) \Rightarrow SE \bot DE \Rightarrow \Delta SDE\) vuông tại E \( \Rightarrow \widehat {SDE} < {90^0}\) )

Vì tam giác ABC vuông cân tại A nên \(AE \bot BC\)

\(\left. \begin{array}{l}AE \bot BC\\SE \bot BC\,\,\left( {SE \bot \left( {ABC} \right)} \right)\end{array} \right\} \Rightarrow BC \bot \left( {SAE} \right)\)

Trong (SAE) kẻ $EF \bot SA\,\,\left( 1 \right)$

Vì \(BC \bot \left( {SAE} \right) \supset EF \Rightarrow EF \bot BC\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra \(d\left( {SA;BC} \right) = EF = \dfrac{{a\sqrt {30} }}{5}\)

Đặt \(SA = SB = SC = b;\,AB = AC = c\)

Vì tam giác ABC vuông cân tại A nên \(BC = AB\sqrt 2  = c\sqrt 2 \)

DE là đường trung bình của tam giác ABC \( \Rightarrow DE = \dfrac{1}{2}AC = \dfrac{c}{2}\)

Xét tam giác vuông SDE và SBE ta có:

\(SD = \sqrt {S{A^2} - A{D^2}}  = \sqrt {{b^2} - \dfrac{{{c^2}}}{4}} \, ;\,SE = \sqrt {S{B^2} - B{E^2}}  = \sqrt {{b^2} - \dfrac{{{c^2}}}{2}} \)

Xét tam giác vuông SDE có:

\(\tan 60 = \dfrac{{SE}}{{DE}} = \dfrac{{\sqrt {{b^2} - \dfrac{{{c^2}}}{2}} }}{{\dfrac{c}{2}}} = \sqrt 3  \Rightarrow {b^2} - \dfrac{{{c^2}}}{2} = \dfrac{{3{c^2}}}{4} \Rightarrow {b^2} = \dfrac{5}{4}{c^2} \Rightarrow b = \dfrac{{c\sqrt 5 }}{2}\)

\( \Rightarrow SE = \sqrt {\dfrac{{5{c^2}}}{4} - \dfrac{{{c^2}}}{2}}  = \dfrac{{c\sqrt 3 }}{2}\)

Áp dụng hệ thức lượng trong tam giác vuông SAE có:$SE.AE = EF.SA \Rightarrow \dfrac{{c\sqrt 3 }}{2}.\dfrac{{c\sqrt 2 }}{2} = \dfrac{{c\sqrt 5 }}{2}.\dfrac{{a\sqrt {30} }}{5} \Rightarrow c = 2a \Rightarrow SE = a\sqrt 3 $

\({S_{\Delta ABC}} = \dfrac{1}{2}A{B^2} = \dfrac{1}{2}{c^2} = 2{a^2}\)

Vậy ${V_{S.ABC}} = \dfrac{1}{3}SE.{S_{\Delta ABC}} = \dfrac{1}{3}a\sqrt 3 .2{a^2} = \dfrac{{2{a^3}\sqrt 3 }}{3}$

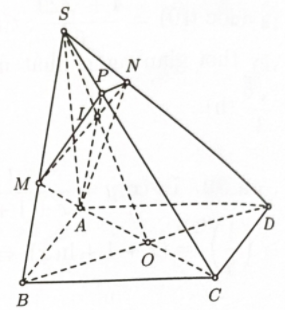
Áp dụng công thức giải nhanh vào bài toán:

Đặt \(a = \dfrac{{SA}}{{SA}} = 1;b = \dfrac{{SB}}{{SM}};c = \dfrac{{SC}}{{SP}} = 5;\)\(d = \dfrac{{SD}}{{SN}}\)

Ta có \(a + c = b + d \Leftrightarrow 1 + 5 = b + d \)\(\Leftrightarrow d = 6 - b\).

\(\dfrac{{{V_{S.AMPN}}}}{{{V_{S.ABCD}}}} = \dfrac{{a + b + c + d}}{{4abcd}}\)\( = \dfrac{{1 + b + 5 + 6 - b}}{{4.1.b.5.(6 - b)}} = \dfrac{3}{5} \cdot \dfrac{1}{{ - {b^2} + 6b}}.\)

Xét \(f(b) = \dfrac{3}{5} \cdot \dfrac{1}{{ - {b^2} + 6b}};b \in [1;5]\).

\({f^\prime }(b) =  - \dfrac{3}{5} \cdot \dfrac{{ - 2b + 6}}{{{{\left( { - {b^2} + 6b} \right)}^2}}};{f^\prime }(b) = 0 \Leftrightarrow b = 3.\)

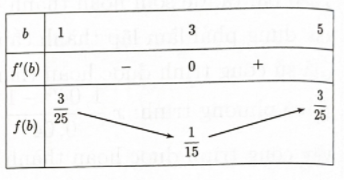
Từ bảng biến thiên (hình bên) ta có giá trị lớn nhất của \(\dfrac{{{V_1}}}{V} = \dfrac{3}{{25}}\).

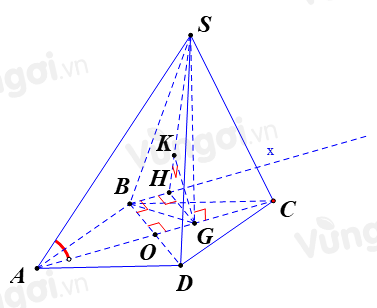
Kẻ Bx song song với AC.

Kẻ GH vuông góc với Bx, GK vuông góc với SH

Bước 1: Chứng minh \(GK \bot \left( {SBH} \right)\)

Ta có:

\(\begin{array}{l}\left. \begin{array}{l}GH \bot BH\\BH \bot SG\end{array} \right\} \Rightarrow BH \bot \left( {SGH} \right)\\\left. \begin{array}{l} \Rightarrow BH \bot GK\\GK \bot SH\end{array} \right\} \Rightarrow GK \bot \left( {SHB} \right)\end{array}\)

Bước 2: Chứng minh \(d\left( {AC,SB} \right) = GK\)

Ta có BH//AC  \( \Rightarrow AC//\left( {SHB} \right)\)

Mà \(SB \subset \left( {SHB} \right)\)

\( =  > d\left( {SB,AC} \right)\)\( = d\left( {AC,\left( {SHB} \right)} \right)\)\( = d\left( {G,\left( {SHB} \right)} \right) = GK\)

Bước 3: Tính GK

Dễ thấy tứ giác OBHG là hình chữ nhật

=> \(HG = OB = \dfrac{a}{2}\)

Áp dụng hệ thức lượng trong tam giác vuông SGH ta có:

\(\dfrac{1}{{G{K^2}}} = \dfrac{1}{{S{G^2}}} + \dfrac{1}{{G{H^2}}}\)\( = \dfrac{1}{{4{a^2}}} + \dfrac{4}{{{a^2}}} = \dfrac{{17}}{{4{a^2}}}\)

\( \Rightarrow GK = \dfrac{{2\sqrt {17} a}}{{17}}\)

Vậy \(d\left( {SB,AC} \right) = \dfrac{{2a\sqrt {17} }}{{17}}\)