Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh bên \(SA = SB = SC\). Góc giữa mặt phẳng (SAB) và mặt đáy bằng \({60^0}\). Biết rằng khoảng cách giữa hai đường thẳng BC và SA bằng \(\dfrac{{a\sqrt {30} }}{5}\), khi đó thể tích khối chóp S.ABC bằng:

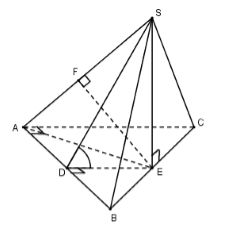
Gọi E là trung điểm của BC

Vì tam giác ABC vuông cân tại A nên E là tâm đường tròn ngoại tiếp tam giác ABC

\( \Rightarrow SE \bot \left( {ABC} \right)\)   

Gọi D là trung điểm của AB ta có DE là đường trung bình của tam giác ABC nên \(DE//AC \Rightarrow DE \bot AB\)

Ta có: \(\left. \begin{array}{l}DE \bot AB\\SE \bot AB\,\,\left( {SE \bot \left( {ABC} \right)} \right)\end{array} \right\} \Rightarrow AB \bot \left( {SDE} \right) \Rightarrow AB \bot SD\)

$\left. \begin{array}{l}\left( {SAB} \right) \cap \left( {ABC} \right) = AB\\\left( {SAB} \right) \supset SD \bot AB\\\left( {ABC} \right) \supset DE \bot AB\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SD;DE} \right)} = \widehat {SDE} = {60^0}$

(Vì \(SE \bot \left( {ABC} \right) \Rightarrow SE \bot DE \Rightarrow \Delta SDE\) vuông tại E \( \Rightarrow \widehat {SDE} < {90^0}\) )

Vì tam giác ABC vuông cân tại A nên \(AE \bot BC\)

\(\left. \begin{array}{l}AE \bot BC\\SE \bot BC\,\,\left( {SE \bot \left( {ABC} \right)} \right)\end{array} \right\} \Rightarrow BC \bot \left( {SAE} \right)\)

Trong (SAE) kẻ $EF \bot SA\,\,\left( 1 \right)$

Vì \(BC \bot \left( {SAE} \right) \supset EF \Rightarrow EF \bot BC\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra \(d\left( {SA;BC} \right) = EF = \dfrac{{a\sqrt {30} }}{5}\)

Đặt \(SA = SB = SC = b;\,AB = AC = c\)

Vì tam giác ABC vuông cân tại A nên \(BC = AB\sqrt 2  = c\sqrt 2 \)

DE là đường trung bình của tam giác ABC \( \Rightarrow DE = \dfrac{1}{2}AC = \dfrac{c}{2}\)

Xét tam giác vuông SDE và SBE ta có:

\(SD = \sqrt {S{A^2} - A{D^2}}  = \sqrt {{b^2} - \dfrac{{{c^2}}}{4}} \, ;\,SE = \sqrt {S{B^2} - B{E^2}}  = \sqrt {{b^2} - \dfrac{{{c^2}}}{2}} \)

Xét tam giác vuông SDE có:

\(\tan 60 = \dfrac{{SE}}{{DE}} = \dfrac{{\sqrt {{b^2} - \dfrac{{{c^2}}}{2}} }}{{\dfrac{c}{2}}} = \sqrt 3  \Rightarrow {b^2} - \dfrac{{{c^2}}}{2} = \dfrac{{3{c^2}}}{4} \Rightarrow {b^2} = \dfrac{5}{4}{c^2} \Rightarrow b = \dfrac{{c\sqrt 5 }}{2}\)

\( \Rightarrow SE = \sqrt {\dfrac{{5{c^2}}}{4} - \dfrac{{{c^2}}}{2}}  = \dfrac{{c\sqrt 3 }}{2}\)

Áp dụng hệ thức lượng trong tam giác vuông SAE có:$SE.AE = EF.SA \Rightarrow \dfrac{{c\sqrt 3 }}{2}.\dfrac{{c\sqrt 2 }}{2} = \dfrac{{c\sqrt 5 }}{2}.\dfrac{{a\sqrt {30} }}{5} \Rightarrow c = 2a \Rightarrow SE = a\sqrt 3 $

\({S_{\Delta ABC}} = \dfrac{1}{2}A{B^2} = \dfrac{1}{2}{c^2} = 2{a^2}\)

Vậy ${V_{S.ABC}} = \dfrac{1}{3}SE.{S_{\Delta ABC}} = \dfrac{1}{3}a\sqrt 3 .2{a^2} = \dfrac{{2{a^3}\sqrt 3 }}{3}$