Cho tứ diện ABCD có \(\widehat {DAB} = \widehat {CBD} = {90^0 };AB = a;AC = a\sqrt 5 ;\widehat {ABC} = \) \({135^0}\). Biết góc giữa hai mặt phẳng \((ABD),(BCD)\) bằng \({30^0}\). Thể tích của tứ diện ABCD bằng

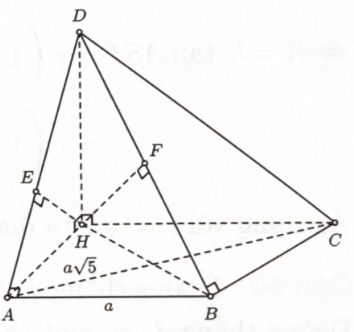
Bước 1: Kẻ \(DH \bot (ABC)\).Chứng minh \(BA \bot AH\) và \(BC \bot BH\)

Kẻ \(DH \bot (ABC)\).

Ta có \(\left\{ {\begin{array}{*{20}{l}}{BA \bot DA}\\{BA \bot DH}\end{array} \Rightarrow BA \bot (DAH)} \right.\)\( \Rightarrow BA \bot AH\).

Tương tự \(\left\{ {\begin{array}{*{20}{l}}{BC \bot DB}\\{BC \bot DH}\end{array} \Rightarrow BC \bot DBH} \right.\)\( \Rightarrow BC \bot BH\).

Bước 2: Tính \({S_{\Delta ABC}}\)

Tam giác AHB có \(AB = a,\widehat {ABH} = {45^0}\)

\( \Rightarrow \Delta HAB\) vuông cân tại \(A \Rightarrow AH = AB = a\).

Áp dụng định lý cosin, ta có \(BC = a\sqrt 2 \).

Vậy \({S_{\Delta ABC}} = \dfrac{1}{2} \cdot BA \cdot BC \cdot \sin \widehat {CBA}\)\( = \dfrac{1}{2} \cdot a \cdot a\sqrt 2  \cdot \dfrac{{\sqrt 2 }}{2} = \dfrac{{{a^2}}}{2}\).

Bước 3: Kẻ \(\left\{ {\begin{array}{*{20}{l}}{HE \bot DA}\\{HF \bot DB}\end{array}} \right.\). Đặt \(DH = x\). Tính HD và thể tích ABCD.

Kẻ \(\left\{ {\begin{array}{*{20}{l}}{HE \bot DA}\\{HF \bot DB}\end{array}} \right.\)

\( \Rightarrow HE \bot (DAB)\) và \(HF \bot (DBC)\).

Suy ra \((\widehat {(DBA),(DBC)}) = \widehat {(HE,HF)} = \widehat {EHF}\) và tam giác HEF vuông tại \(E\).

Đặt \(DH = x\), khi đó \(HE = \dfrac{{ax}}{{\sqrt {{a^2} + {x^2}} }},HF = \dfrac{{xa\sqrt 2 }}{{\sqrt {2{a^2} + {x^2}} }}\).

Suy ra \(\cos \widehat {EHF} = \dfrac{{HE}}{{HF}} = \sqrt {\dfrac{3}{4}} \)\( = \dfrac{{\sqrt {{x^2} + 2{a^2}} }}{{\sqrt {2{x^2} + 2{a^2}} }} \Rightarrow x = a\).

Vậy \({V_{ABCD}} = \dfrac{1}{3}.DH.{S_{\Delta ABC}} = \dfrac{{{a^3}}}{6}\).