Câu hỏi:
2 năm trước
Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là \(V\). Gọi \(P\) là điểm trên cạnh SC sao cho \(SC = 5SP\). Mặt phẳng \((\alpha )\) qua A P cắt hai cạnh SB và SD lần lượt tại \(M\) và \(N\). Gọi \({V_1}\) là thể tích của khối chóp S.AMPN. Giá trị lớn nhất của \(\dfrac{{{V_1}}}{V}\) bằng
Trả lời bởi giáo viên
Đáp án đúng: c
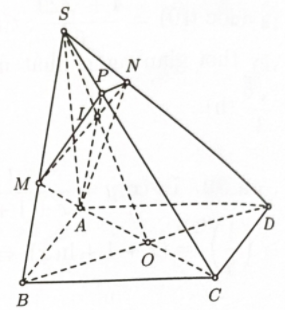
Áp dụng công thức giải nhanh vào bài toán:
Đặt \(a = \dfrac{{SA}}{{SA}} = 1;b = \dfrac{{SB}}{{SM}};c = \dfrac{{SC}}{{SP}} = 5;\)\(d = \dfrac{{SD}}{{SN}}\)
Ta có \(a + c = b + d \Leftrightarrow 1 + 5 = b + d \)\(\Leftrightarrow d = 6 - b\).
\(\dfrac{{{V_{S.AMPN}}}}{{{V_{S.ABCD}}}} = \dfrac{{a + b + c + d}}{{4abcd}}\)\( = \dfrac{{1 + b + 5 + 6 - b}}{{4.1.b.5.(6 - b)}} = \dfrac{3}{5} \cdot \dfrac{1}{{ - {b^2} + 6b}}.\)
Xét \(f(b) = \dfrac{3}{5} \cdot \dfrac{1}{{ - {b^2} + 6b}};b \in [1;5]\).
\({f^\prime }(b) = - \dfrac{3}{5} \cdot \dfrac{{ - 2b + 6}}{{{{\left( { - {b^2} + 6b} \right)}^2}}};{f^\prime }(b) = 0 \Leftrightarrow b = 3.\)
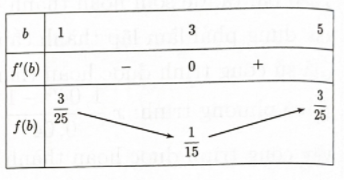
Từ bảng biến thiên (hình bên) ta có giá trị lớn nhất của \(\dfrac{{{V_1}}}{V} = \dfrac{3}{{25}}\).
Hướng dẫn giải:
- Công thức giải nhanh (chỉ áp dụng với hình chóp có đáy là hình bình hành):
Hình chóp S . ABCD có \(\dfrac{{SM}}{{SA}} = a;\dfrac{{SN}}{{SB}} = b;\dfrac{{SP}}{{SC}} = c;\dfrac{{SQ}}{{SD}} = d.\) Khi đó, \(\dfrac{1}{a} + \dfrac{1}{c} = \dfrac{1}{b} + \dfrac{1}{d} \Rightarrow \dfrac{{{S_{S.MNPQ}}}}{{{V_{S.ABCD}}}} = \dfrac{{abcd}}{4}\left( {\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} + \dfrac{1}{d}} \right).\)
- Xét \(f(b) = \dfrac{3}{5} \cdot \dfrac{1}{{ - {b^2} + 6b}};b \in [1;5]\). Lập bảng biến thiên và tìm giá trị lớn nhất của \(\dfrac{{{V_1}}}{V}\).
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
