Cho \({z_1};{z_2};{z_3}\) là ba số phức thay đổi thỏa mãn $\left| {{z_1}} \right| = 2;\,\,\left| {{z_3}} \right| = 1$ và \({z_2} = {z_1}{z_3}\). Trong mặt phẳng phức A, B biểu diễn \({z_1};{z_2}\). Giả sử O, A, B lập thành tam giác có diện tích là a, chu vi là b. Giá trị lớn nhất của biểu thức \(T = a + b\) là:
Trả lời bởi giáo viên
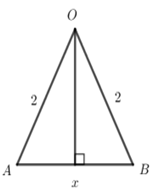
Ta có \(\left| {{z_2}} \right| = \left| {{z_1}} \right|\left| {{z_3}} \right| = 2 \Rightarrow OB = OA = 2\).
Đặt \(AB = x\,\,\left( {0 < x < 4} \right)\) ta có: \(a = \dfrac{1}{2}.x.\sqrt {4 - \dfrac{{{x^2}}}{4}} = \dfrac{1}{4}x\sqrt {16 - {x^2}} ;\,\,b = 2 + 2 + x = 4 + x\)
\( \Rightarrow T = a + b = \dfrac{{x\sqrt {16 - {x^2}} }}{4} + 4 + x\)
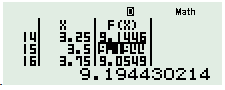
Sử dụng MTCT ta tính được \({T_{\max }} \approx 9,19\)
Hướng dẫn giải:
+) Đặt \(AB = x\,\,\left( {0 < x < 4} \right)\). Tính diện tích và chu vi tam giác OAB theo x.
+) Viết \(T = f\left( x \right)\). Tìm GTLN của \(f\left( x \right)\)