Tìm m để phương trình ${4^{\sqrt {x + 1}  + \sqrt {3 - x} }} - {14.2^{\sqrt {x + 1}  + \sqrt {3 - x} }} + 8 = m$ có nghiệm

Điều kiện: $\left\{ \begin{array}{l}x + 1 \ge 0\\3 - x \ge 0\end{array} \right. \Leftrightarrow  - 1 \le x \le 3.$

Đặt $t = {2^{\sqrt {x + 1}  + \sqrt {3 - x} }} = t(x)\,\,\left( {t\left( x \right) > 0} \right)$.Ta có $t'\left( x \right) = \left( {\dfrac{1}{{2\sqrt {x + 1} }} - \dfrac{1}{{2\sqrt {3 - x} }}} \right){.2^{\sqrt {x + 1}  + \sqrt {3 - x} }}\ln 2.$

$\Rightarrow t'(x) = 0 \Leftrightarrow \dfrac{1}{{2\sqrt {x + 1} }} - \dfrac{1}{{2\sqrt {3 - x} }} \Leftrightarrow \sqrt {x + 1}  = \sqrt {3 - x}  \Leftrightarrow x = 1.$

Bảng biến thiên

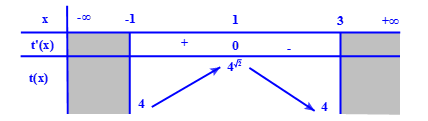
Do đó $t \in \left[ {4;{4^{\sqrt 2 }}} \right]$.

Yêu cầu bài toán trở thành: Tìm m để phương trình ${t^2} - 14t + 8 = m\,\,(*)$ có nghiệm với $t \in \left[ {4;{4^{\sqrt 2 }}} \right]$.

Xét hàm số $g(t) = {t^2} - 14t + 8,\,\,t \in \left[ {4;{4^{\sqrt 2 }}} \right].$

Ta có $g'(t) = 2t - 14,\,\,g'(t) = 0 \Leftrightarrow 2t - 14 = 0 \Leftrightarrow t = 7$

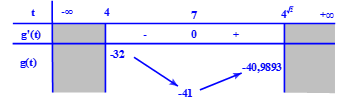
Dựa vào bảng biến thiên ta được giá trị m cần tìm là $- 41 \le m \le  - 32.$