Biết rằng tập hợp tất cả các giá trị thực của tham số \(m\) để phương trình \({(2 + \sqrt 3 )^x} + m{(2 - \sqrt 3 )^x} = 1\) có hai nghiệm phân biệt là khoảng \((a;b)\). Tính \(T = \) \(3a + 8b\).

Đặt \(t = {(2 + \sqrt 3 )^x},t > 0\)\( \Rightarrow {(2 - \sqrt 3 )^x} = \dfrac{1}{t}\).

Khi đó phương trình trở thành \(t + m \cdot \dfrac{1}{t} = 1\)\( \Leftrightarrow {t^2} + m = t \Leftrightarrow m =  - {t^2} + t\)\( \Leftrightarrow m = f(t)\).

Bài toán tương đương: Tìm \(m\) để phương trình \(m = f(t)\) có hai nghiệm dương phân biệt.

Ta có \(f(t) =  - {t^2} + t\)\( \Rightarrow {f^\prime }(t) =  - 2t + 1;\)

\({f^\prime }(t) = 0 \Leftrightarrow t = \dfrac{1}{2} > 0\).

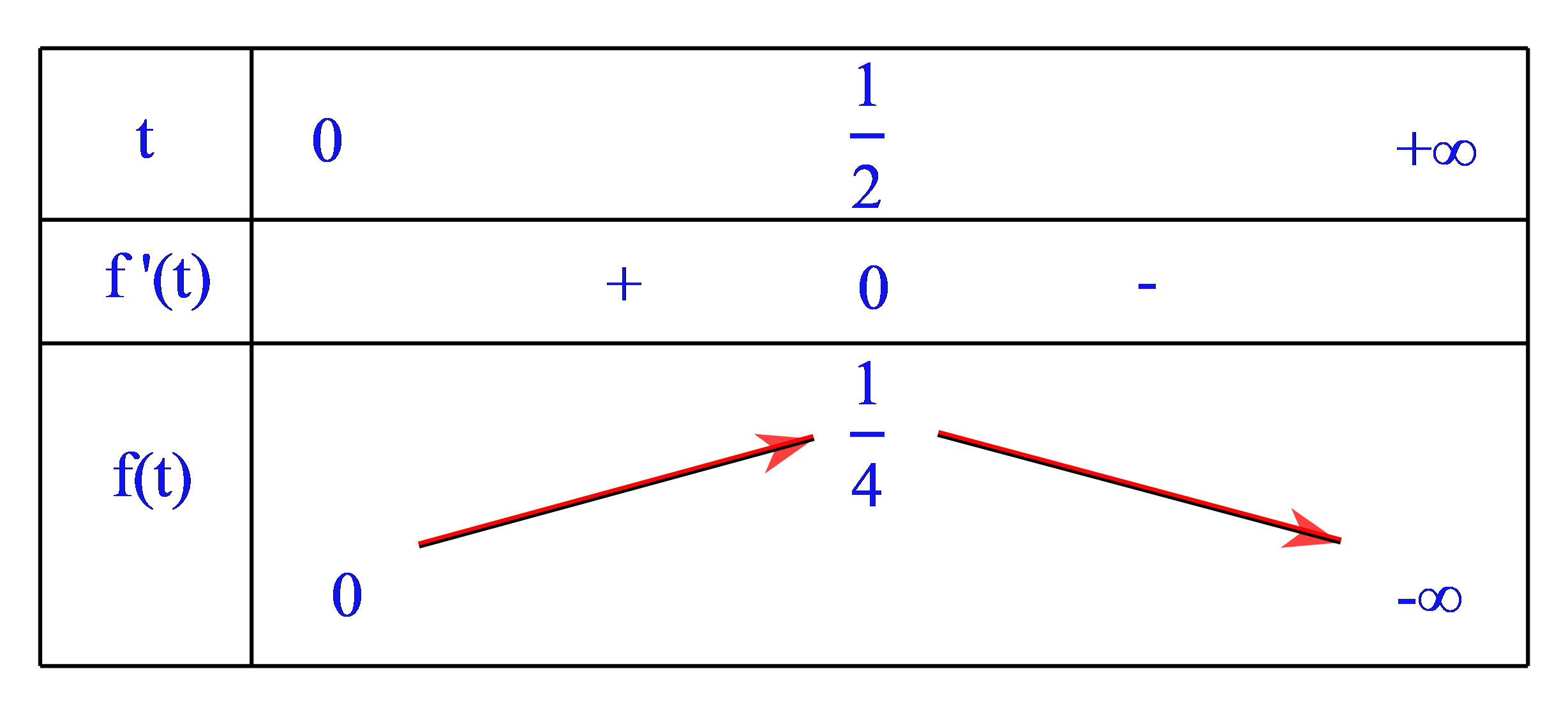
Dựa vào bảng biến thiên ta thấy phương trình có 2 nghiệm khi \(0 < m < \dfrac{1}{4}\).

Vậy \(m \in \left( {0;\dfrac{1}{4}} \right)\) từ đó ta có \(a = 0,b = \dfrac{1}{4}\)

\( \Rightarrow T = 3a + 8b = 2\).