Câu hỏi:
2 năm trước
- Xét các số phức \(z\) thỏa mãn \(|z - 1 + 2i| = \sqrt 5 \). Tìm số phức \(w\) có mô đun lớn nhất, biết rằng \(w = z + 1 + i\).
- Mô đun của một số phức là khoảng cách từ điểm O đến điểm biểu diễn số phức đó.
Trả lời bởi giáo viên
Đáp án đúng: a
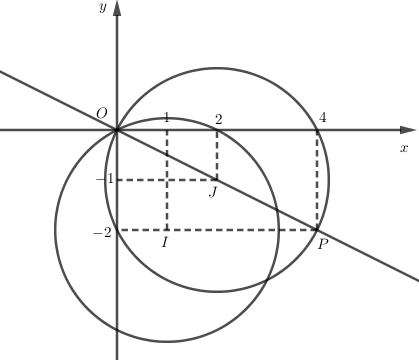
Các điểm $M\left( {x;y} \right)$ biểu diễn số phức \(z\) thỏa mãn \(|z - (1 - 2i)| = \sqrt 5 \) thuộc đường tròn tâm $I(1;-2)$ (biểu diễn số phức \(z_2=1-2i\)) bán kính bằng \(\sqrt 5 \).
Ta có \(w = z + 1 + i\) nên \(z=w-1-i\). Thay vào \(|z - 1 + 2i| = \sqrt 5 \) ta được:
\(|(w-1-i )- 1 + 2i| = \sqrt 5 \) hay \(|w-(2-i)|=\sqrt 5\)
Từ đó các điểm biểu diễn $w$ thuộc đường tròn tâm J(2;-1) (điểm biểu diễn số phức 2-i) bán kính \(\sqrt 5 \)
Thay tọa độ điểm O vào \(|w-(2-i)|=\sqrt 5\) ta thấy \(\left| {2 - i} \right| = \sqrt 5 \) nên đường tròn này đi qua gốc $O$.
Quan sát hình vẽ trên ta thấy để w có mô đun lớn nhất thì khoảng cách từ O đến điểm trên đường tròn tâm J bán kính \(\sqrt 5 \) lớn nhất hay $OP$ là đường kính của đường tròn đó, tức P đối xứng với O qua J, vậy $w = 2\left( {2 - i} \right) = 4 - 2i$
Hướng dẫn giải:
Điểm biểu diễn z thỏa mãn \(|z-z_1|=\sqrt{5}\) là đường tròn tâm $I$ (biểu diễn \(z_1\)), bán kính \(\sqrt{5}\)
Câu hỏi khác
- Bài tập số phức và các phép toán cộng, trừ, nhân, chia số phức toán 12 có lời giải
- Bài tập phương trình bậc hai với hệ số thực (căn bậc hai của số phức) toán 12 có lời giải
- Bài tập điểm biểu diễn số phức thỏa mãn điều kiện cho trước có lời giải MÔN TOÁN Lớp 12
- Bài tập tìm min, max liên quan đến số phức có lời giải MÔN TOÁN Lớp 12
- Bài tập dạng lượng giác của số phức toán 12 có lời giải
