Cho 2 số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1} + 3} \right| + \left| {{z_1} - 3} \right|\)\( = \left| {{z_2} + 4} \right| + \left| {{z_2} - 4} \right| = 10\). Tính giá trị lớn nhất của biểu thức \(\left| {{z_1} - {z_2}} \right|\)

Bước 1: Tìm quỹ tích điểm biểu diễn \({z_1},{z_2}\)

Ta có:

\( + )\left| {{z_1} + 3} \right| + \left| {{z_1} - 3} \right| = 10\)

\( \Rightarrow c = 3,a = 5\)\( \Rightarrow b = \sqrt {{a^2} - {c^2}}  = 4\)

\( \Rightarrow \) tập hợp biểu diễn số phức \({z_1}\) là elip có phương trình \(\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{16}} = 1\left( {{E_1}} \right)\).

+) \(\left| {{z_2} + 4} \right| + \left| {{z_2} - 4} \right| = 10\)

\( \Rightarrow a = 5,c = 4 \Rightarrow b = 3\)

\( \Rightarrow \) Tập hợp biểu diễn số phức \({z_2}\) là Elip có phương trình \(\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1\left( {{E_1}} \right)\).

Bước 2: Gọi \(M\) là điểm biểu diễn \({z_1},N\) là điểm biểu diễn số phức \({z_2}\). Gọi \(P = MN \cap \left( {{E_1}} \right)\). Tìm \(\max \left| {{z_1} - {z_2}} \right|\)

Đồ thị của \(\left( {{E_1}} \right)\) và \(\left( {{E_2}} \right)\):

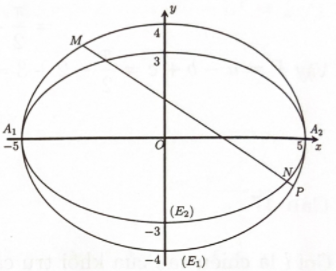
Gọi \(M\) là điểm biểu diễn \({z_1},N\) là điểm biểu diễn số phức \({z_2}\).

Khi đó \(\left| {{z_1} - {z_2}} \right| = MN\).

Gọi \(P = MN \cap \left( {{E_1}} \right)\)

\( \Rightarrow MN \le MP \le {A_1}{A_2} = 10\) (không đổi).

\( \Rightarrow \max \left| {{z_1} - {z_2}} \right| = \max MN = 10\).