Cho hai số phức ${z_1},{\rm{ }}\,{z_2}$ thỏa mãn \(\left| {{z_1} - 2i} \right| = 3\) và \(\left| {{z_2} + 2 + 2i} \right| = \left| {{z_2} + 2 + 4i} \right|\). Giá trị nhỏ nhất của biểu thức \(P = \left| {{z_1} - {z_2}} \right|\) bằng:
Trả lời bởi giáo viên
Đặt ${z_1} = {x_1} + {y_1}i$ và ${z_2} = {x_2} + {y_2}i$ với ${x_1},{\rm{ }}{x_2},{\rm{ }}{y_1},{\rm{ }}{y_2} \in \mathbb{R}.$
\(\left| {{z_1} - 2i} \right| = 3 \to {x_1}^2 + {\left( {{y_1} - 2} \right)^2} = 9\) suy ra tập hợp các số phức \({z_1}\) là đường tròn \(\left( C \right):{x^2} + {\left( {y - 2} \right)^2} = 9\).
\(\left| {{z_2} + 2 + 2i} \right| = \left| {{z_2} + 2 + 4i} \right|\)
\( \to {\left( {{x_2} + 2} \right)^2} + {\left( {{y_2} + 2} \right)^2} = {\left( {{x_2} + 2} \right)^2} + {\left( {{y_2} + 4} \right)^2}\)
\( \Leftrightarrow {y_2} + 3 = 0\) suy ra tập hợp các số phức \({z_2}\) là đường thẳng \(d:y = - 3\).
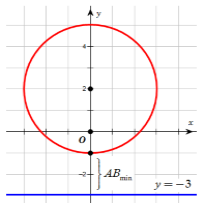
Ta có \(P = \left| {{z_1} - {z_2}} \right| = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \). Đây chính là khoảng cách từ điểm $B\left( {{x_2};{y_2}} \right) \in d$ đến điểm $A\left( {{x_1};{y_1}} \right) \in \left( C \right)$.
Do đó ${\left| {{z_2} - {z_1}} \right|_{\min }} \Leftrightarrow A{B_{\min }}.$
Dựa vào hình vẽ ta tìm được $A{B_{\min }} = 2$ khi \(A\left( {0; - 1} \right),{\rm{ }}B\left( {0; - 3} \right)\).
Hướng dẫn giải:
Gọi \({z_1} = {x_1} + {y_1}i,{z_2} = {x_2} + {y_2}i\), thay vào điều kiện đề bài tìm mối liên hệ \({x_1},{y_1},{x_2},{y_2}\).
Áp dụng phương pháp hình học để tìm điều kiện cho \(\left| {{z_1} - {z_2}} \right|\) đạt GTNN.

