Cho hai số phức \({z_1},\,\,{z_2}\) thỏa mãn \(\left| {{z_1} + 3 + 2i} \right| = 1\) và \(\left| {{z_2} + 2 - i} \right| = 1\). Xét các số phức \(z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right)\) thỏa mãn \(2a - b = 0\). Khi đó biểu thức \(T = \left| {z - {z_1}} \right| + \left| {z - 2{z_2}} \right|\) đạt giá trị nhỏ nhất thì giá trị biểu thức \(P = {a^2} + {b^2}\) bằng:
Gọi \({M_1},\,\,{M_2},\,\,M\) lần lượt là các điểm biểu diễn số phức \({z_1},\,\,2{z_2},\,\,z\).
Ta có:
+) \(\left| {{z_1} + 3 + 2i} \right| = 1 \Leftrightarrow \left| {{z_1} - \left( { - 3 - 2i} \right)} \right| = 1\).
\( \Rightarrow \) Tập hợp các điểm \({M_1}\) là đường tròn \(\left( {{C_1}} \right)\) tâm \({I_1}\left( { - 3; - 2} \right)\), bán kính \({R_1} = 1\).
+) \(\left| {{z_2} + 2 - i} \right| = 1 \Leftrightarrow \left| {2{z_2} - \left( { - 4 + 2i} \right)} \right| = 2\)
\( \Rightarrow \) Tập hợp các điểm \({M_2}\) là đường tròn \(\left( {{C_2}} \right)\) tâm \({I_2}\left( { - 4;2} \right)\), bán kính \({R_2} = 2\).
+) số phức \(z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right)\) thỏa mãn \(2a - b = 0\)
\( \Rightarrow \) Tập hợp các điểm \(M\) là đường thẳng \(d:\,\,2x - y = 0\).
Khi đó ta có: \(T = \left| {z - {z_1}} \right| + \left| {z - 2{z_2}} \right| = M{M_1} + M{M_2}\).
Gọi \(\left( {{C_3}} \right)\) đối xứng \(\left( {{C_1}} \right)\) qua d \( \Rightarrow \left( {{C_3}} \right)\) có tâm \({I_3}\left( {\dfrac{1}{5};\dfrac{{ - 18}}{5}} \right)\), bán kính \({R_3} = 1\).
Gọi \({M_3}\) đối xứng \({M_1}\) qua \(d\) \({M_3} \in \left( {{C_3}} \right)\).
Khi đó ta có: \(M{M_1} + M{M_2} = M{M_3} + M{M_2}\).
Gọi A, B lần lượt là giao điểm của \({I_2}{I_3}\) với \(\left( {{C_2}} \right),\,\,\left( {{C_3}} \right)\).
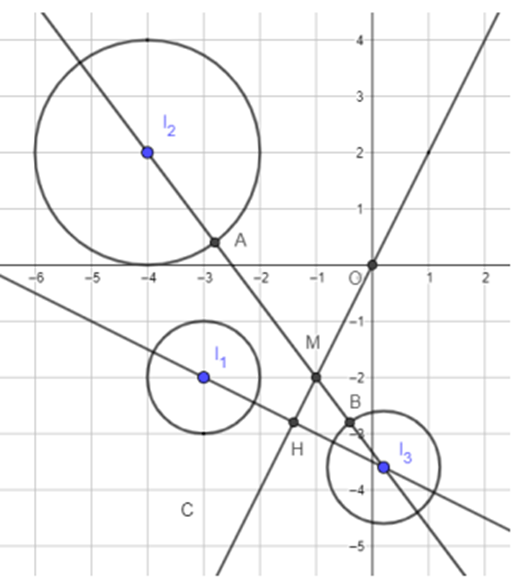
Ta có: \(M{M_2} + M{M_3} \ge AB\). Dấu “=” xảy ra khi \({M_1} \equiv A,\,\,{M_3} \equiv B\).
Khi đó \({P_{\min }} = AB = {I_2}{I_3} - 3 \)\(= \sqrt {{{\left( {\dfrac{1}{5} + 4} \right)}^2} + {{\left( { - \dfrac{{18}}{5} - 2} \right)}^2}} - 3 = 4\).
Khi đó \(M = {I_2}{I_3} \cap d \Rightarrow M\left( { - 1; - 2} \right)\).
Vậy \(a = - 1,\,\,b = - 2\) nên \({a^2} + {b^2} = 5\).
Đề thi THPT QG - 2021 - mã 102
Xét các số phức \(z,\,{\rm{w}}\) thỏa mãn \(|z|\, = 1\) và \(|{\rm{w}}|\, = 2.\) Khi \(\left| {z + i\overline {\rm{w}} + 6 - 8i} \right|\) đạt giá trị nhỏ nhất, \(\left| {z - {\rm{w}}} \right|\) bằng
Gọi \(M\) và \(N\) lần lượt là các điểm biểu diễn số phức \(z + 6 - 8i\) và \( - i\overline {\rm{w}} \).
Ta có: \(\left| z \right| = 1 \Leftrightarrow \left| {\left( {z + 6 - 8i} \right) + \left( { - 6 + 8i} \right)} \right| = 1 \Leftrightarrow MI = 1\) với \(I\left( {6; - 8} \right).\)
Suy ra tập hợp điểm \(M\) là đường tròn \(\left( {{T_1}} \right)\) tâm \(I\left( {6; - 8} \right)\) và bán kính \({R_1} = 1\).
Ta có: \(\left| { - i\overline {\rm{w}} } \right| = \left| { - i} \right|.\left| {\overline {\rm{w}} } \right| = 2.\)
Suy ra tập hợp điểm \(N\) là đường tròn \(\left( {{T_2}} \right)\) tâm \(O\) và bán kính \({R_2} = 2\).
Ta có: \(P = \left| {z + \overline {iw} + 6 - 8i} \right| = MN\)
\( \Rightarrow \min P = OI - {R_1} - {R_2} = 10 - 1 - 2 = 7\) (do \(\left( {{T_1}} \right)\) và \(\left( {{T_2}} \right)\) rời nhau).
Ta có: \(\left\{ \begin{array}{l}\overrightarrow {OM} = \dfrac{9}{{10}}\overrightarrow {OI} \\\overrightarrow {ON} = \dfrac{1}{5}\overrightarrow {OI} \end{array} \right. \Rightarrow \left\{ \begin{array}{l}M\left( {\dfrac{{27}}{5}; - \dfrac{{36}}{5}} \right)\\N\left( {\dfrac{6}{5}; - \dfrac{8}{5}} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}z + 6 - 8i = \dfrac{{27}}{5} - \dfrac{{36}}{5}i\\ - i\overline {\rm{w}} = \dfrac{6}{5} - \dfrac{8}{5}i\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}z = - \dfrac{3}{5} + \dfrac{4}{5}i\\{\rm{w}} = \dfrac{8}{5} - \dfrac{6}{5}i\end{array} \right.\)
Vậy \(\left| {z - {\rm{w}}} \right| = \left| { - \dfrac{{11}}{5} + 2i} \right| = \dfrac{{\sqrt {221} }}{5}\)
Với hai số phức bất kì ${z_1},{z_2}$ , khẳng định nào sau đây đúng:
Ta có: \(\left| {\left| {{z_1}} \right| - \left| {{z_2}} \right|} \right| \le \left| {{z_1} \pm {z_2}} \right| \le \left| {{z_1}} \right| + \left| {{z_2}} \right|\) nên A đúng.
Cho số phức $z$ thỏa mãn điều kiện \(\left| {z - 2 + 2i} \right| = 1\). Tìm giá trị lớn nhất của\(\left| z \right|\)
Áp dụng bất đẳng thức chứa dấu giá trị tuyệt đối ta có:
\(1 = \left| {z - 2 + 2i} \right| = \left| {z - \left( {2 - 2i} \right)} \right| \ge \left| z \right| - \left| {2 - 2i} \right| = \left| z \right| - 2\sqrt 2 \Rightarrow \left| z \right| \le 1 + 2\sqrt 2 \)
Vậy \(\max \left| z \right| = 1 + 2\sqrt 2 \)
Cho số phức $z$ thỏa mãn \(|z - 2 - 2i| = 1\). Số phức \(z - i\) có mô đun nhỏ nhất là:
Ta có: \(\left| {z - i} \right| = \left| {\left( {z - 2 - 2i} \right) + \left( {i + 2} \right)} \right| \ge \left| {\left| {z - 2 - 2i} \right| - \left| {i + 2} \right|} \right| = \left| {1 - \sqrt 5 } \right| = \sqrt 5 - 1\)
Vậy \(\left| {z - i} \right| \ge \sqrt 5 - 1\) nên \(\min \left| {z - i} \right| = \sqrt 5 - 1\)
Xác định số phức \(z\) thỏa mãn \(|z - 2 - 2i| = \sqrt 2 \) mà \(|z|\) đạt giá trị lớn nhất.
Sử dụng bất đẳng thức chứa dấu giá trị tuyệt đối ta có:
\(\sqrt 2 = |z - 2 - 2i| \ge |z| - | - 2 - 2i| = |z| - 2\sqrt 2 \Rightarrow |z| \le 3\sqrt 2 \)
Suy ra \(\max |z| = 3\sqrt 2 \).
Kiểm tra các đáp án đã cho chỉ có đáp án C thỏa mãn.
Cho số phức \(z\) có \(|z| = 2\) thì số phức \(w = z + 3i\) có mô đun nhỏ nhất và lớn nhất lần lượt là
Sử dụng bất đẳng thức chứa dấu giá trị tuyệt đối ta có
\(\left| {|z| - |3i|} \right| \le |z + 3i| \le \left| {|z| + |3i|} \right| \Leftrightarrow |2 - 3| \le |w| \le |2 + 3| \Leftrightarrow 1 \le |w| \le 5\)
Nhận thấy với \(z = - 2i\) thì \(\left| w \right| = 1\) và với \(z = 2i\) thì \(\left| w \right| = 5\) nên \(1\) và \(5\) là GTNN và GTLN của \(\left| w \right|\).
Cho số phức \(z\) thoả \(|z - 3 + 4i| = 2\) và \(w = 2z + 1 - i\). Khi đó \(|w|\) có giá trị lớn nhất là:
Ta có \(|z - 3 + 4i| = 2 \Leftrightarrow |2z - 6 + 8i| = 4.\)
Theo bất đẳng thức chứa dấu giá trị tuyệt đối có
\(4 = |2z - 6 + 8i| = |(2z + 1 - i) - (7 - 9i)| \ge |2z + 1 - i| - |7 - 9i| = |w| - \sqrt {130} \)
\( \Rightarrow |w| - \sqrt {130} \le 4 \Rightarrow |w| \le 4 + \sqrt {130} \)
Cho số phức \(z\) thỏa mãn \(|{z^2} - i| = 1\). Tìm giá trị lớn nhất của \(|\bar z|\).
Theo bất đẳng thức chứa dấu giá trị tuyệt đối ta có \(1 = \left| {{z^2} - i} \right| \ge \left| {{z^2}} \right| - \left| i \right| = {\left| z \right|^2} - 1 \Rightarrow {\left| z \right|^2} \le 2 \Rightarrow \left| z \right| = \left| {\overline z } \right| \le \sqrt 2 \)
Cho số phức \(z\) thỏa mãn\(|z - 1 - 2i| = 4\). Gọi $M,m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của \(|z + 2 + i|\). Tính \(S = {M^2} + {m^2}\).
Theo bất đẳng thức chứa dấu giá trị tuyệt đối ta có
\(|z + 2 + i| = |(z - 1 - 2i) + (3 + 3i)| \ge ||z - 1 - 2i| - |3 + 3i|| = |4 - 3\sqrt 2 | = 3\sqrt 2 - 4 = m\)
\(|z + 2 + i| = |(z - 1 - 2i) + (3 + 3i)| \le |z - 1 - 2i| + |3 + 3i| = 4 + 3\sqrt 2 = M\)
Suy ra \({M^2} + {m^2} = {(3\sqrt 2 - 4)^2} + {(4 + 3\sqrt 2 )^2} = 2({4^2} + {(3\sqrt 2 )^2}) = 68\)
Cho số phức \(z\) có điểm biểu diễn nằm trên đường thẳng \(3x - 4y - 3 = 0\), $\left| z \right|$ nhỏ nhất bằng.
Giả sử \(z = x + yi\), ta có \(3x - 4y - 3 = 0\), suy ra \(y = \dfrac{3}{4}\left( {x - 1} \right)\)
Ta có \(|z| = \sqrt {{x^2} + {y^2}} = \sqrt {{x^2} + \dfrac{9}{{16}}{{(x - 1)}^2}} = \dfrac{1}{4}\sqrt {16{x^2} + 9{{(x - 1)}^2}} \) \( = \dfrac{1}{4}\sqrt {25{x^2} - 18x + 9} = \dfrac{1}{4}\sqrt {{{\left( {5x - \dfrac{9}{5}} \right)}^2} + \dfrac{{144}}{{25}}} \ge \dfrac{1}{4}.\dfrac{{12}}{5} = \dfrac{3}{5}\)
Dấu “=” xảy ra khi \(x = \dfrac{9}{{25}}\) và \(y = - \dfrac{{12}}{{25}}\).
Cho số phức \(z\) thỏa mãn \(|z + 3| + |z - 3| = 10\). Giá trị nhỏ nhất của \(|z|\) là:
Giả sử \(z = a + bi\), theo giả thiết ta có
\(|a + bi + 3| + |a + bi - 3| = 10 \Leftrightarrow \sqrt {{{(a + 3)}^2} + {b^2}} + \sqrt {{{(a - 3)}^2} + {b^2}} = 10\)
Áp dụng bất đẳng thức Bunhiacopxki với $A=1;B=1;X=\sqrt {{{(a + 3)}^2} + {b^2}} ;$$Y=\sqrt {{{(a - 3)}^2} + {b^2}} $ ta có
\(10 = 1.\sqrt {{{(a + 3)}^2} + {b^2}} + 1.\sqrt {{{(a - 3)}^2} + {b^2}} \)\(\le \sqrt {({1^2} + {1^2})[{{(a + 3)}^2} + {b^2} + {{(a - 3)}^2} + {b^2}]} \) \( = \sqrt {2.[2{a^2} + 2{b^2} + 18]} = 2\sqrt {{a^2} + {b^2} + 9} \)
Suy ra \(\sqrt {{a^2} + {b^2} + 9} \ge 5 \Leftrightarrow {a^2} + {b^2} + 9 \ge 25 \Leftrightarrow {a^2} + {b^2} \ge 16\)
Do đó \(|z| = \sqrt {{a^2} + {b^2}} \ge 4\)
Cho \({z_1},{z_2}\) thỏa mãn \(|{z_1} - {z_2}| = 1\) và \(|{z_1} + {z_2}| = 3\). Tính \(\max T = |{z_1}| + |{z_2}|\)
Giả sử \({z_1} = {x_1} + {y_1}i\),\({z_2} = {x_2} + {y_2}i\).
Theo giả thiết \(|{z_1} - {z_2}| = 1\) có
\({({x_1} - {x_2})^2} + {({y_1} - {y_2})^2} = 1 \Leftrightarrow x_1^2 + x_2^2 - 2{x_1}{x_2} + y_1^2 + y_2^2 - 2{y_1}{y_2} = 1\) (1)
Theo giả thiết \(|{z_1} + {z_2}| = 3\) có
\({({x_1} + {x_2})^2} + {({y_1} + {y_2})^2} = 9 \Leftrightarrow x_1^2 + x_2^2 + 2{x_1}{x_2} + y_1^2 + y_2^2 + 2{y_1}{y_2} = 9\) (2)
Cộng vế với vế của (1) và (2) ta có
\(x_1^2 + x_2^2 + y_1^2 + y_2^2 = 5\)
Ta có
\(T = \sqrt {x_1^2 + y_1^2} + \sqrt {x_2^2 + y_2^2} \)
Theo bất đẳng thức Bunhiacopxki ta có
\(T \le \sqrt {2.(x_1^2 + x_2^2 + y_1^2 + y_2^2)} = \sqrt {10} \)
Tìm giá trị nhỏ nhất của \(|z|\), biết rằng \(z\) thỏa mãn điều kiện \(|\dfrac{{4 + 2i}}{{1 - i}}z - 1| = 1\).
Có \(\dfrac{{4 + 2i}}{{1 - i}} = 1 + 3i\). Đặt \(z = x + yi\) thì
\(\dfrac{{4 + 2i}}{{1 - i}}z - 1 = (1 + 3i)(x + yi) - 1 = (x - 3y - 1) + (3x + y)i\)
Điều kiện đã cho trong bài được viết lại thành
\({(x - 3y - 1)^2} + {(3x + y)^2} = 1\)
\( \Leftrightarrow {(x - 3y)^2} - 2(x - 3y) + 1 + {(3x + y)^2} = 1\)
\( \Leftrightarrow 10{x^2} + 10{y^2} - 2x + 6y = 0\)
\( \Leftrightarrow \left( {{x^2} - \dfrac{1}{5}x} \right) + \left( {{y^2} + \dfrac{3}{5}y} \right) = 0\)
\( \Leftrightarrow {\left( {x - \dfrac{1}{{10}}} \right)^2} + {\left( {y + \dfrac{3}{{10}}} \right)^2} = \dfrac{1}{{10}}\) (*)
Điểm biểu diễn \(M(x,y)\) của \(z\) chạy trên đường tròn (*). Cần tìm điểm \(M(x,y)\) thuộc đường tròn này để $OM$ nhỏ nhất.
Vì đường tròn này qua $O$ nên min $OM = 0$ khi \(M \equiv O\) hay $M\left( {0,0} \right)$, do đó $z = 0$ hay $min\left| z \right| = 0$.
Tìm giá trị lớn nhất của \(|z|\), biết rằng \(z\) thỏa mãn điều kiện \(|\dfrac{{ - 2 - 3i}}{{3 - 2i}}z + 1| = 1\).
Có \(\dfrac{{ - 2 - 3i}}{{3 - 2i}} = - i\). Đặt \(z = x + yi\) thì
\(\dfrac{{ - 2 - 3i}}{{3 - 2i}}z + 1 = - i(x + yi) + 1 = (y + 1) - xi\)
Điều kiện đã cho trong bài được viết lại thành \({(y + 1)^2} + {x^2} = 1\)
Điểm biểu diễn \(M(x,y)\) của \(z\) chạy trên đường tròn (*) có tâm $I\left( {0, - 1} \right)$, bán kính bằng $1$.
Cần tìm điểm \(M(x,y)\) thuộc đường tròn này để $OM$ lớn nhất.
Vì \(O\) nằm trên đường tròn nên $OM$ lớn nhất khi $OM$ là đường kính của (*) \( \Leftrightarrow \) $I$ là trung điểm của $OM$ \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2{x_I}}&{}\\{y = 2{y_I}}&{}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}&{}\\{y = - 2}&{}\end{array}} \right. \Leftrightarrow M(0, - 2)\). Suy ra \(z = - 2i \Leftrightarrow |z| = 2\)
Vậy $\max \left| z \right| = 2$
Trong số các số phức $z$ thỏa mãn điều kiện \(\left| {z - 4 + 3i} \right| = 3\), gọi ${z_0}$ là số phức có mô đun lớn nhất. Khi đó \(\left| {{z_0}} \right|\) là
Gọi $z = x + yi$;
Khi đó $z - 4 + 3i = \left( {x - 4} \right) + \left( {y + 3} \right)i$
$ \Rightarrow \left| {z - 4 + 3i} \right| = \left| {\left( {x - 4} \right) + \left( {y + 3} \right)i} \right| = 3 \Rightarrow {\left( {x - 4} \right)^2} + {\left( {y + 3} \right)^2} = 9$
Vậy quỹ tích các điểm \(M\) biểu diễn số phức \(z\) thuộc đường tròn tâm $I\left( {4; - 3} \right);R = 3$.
Đặt $\left\{ \begin{array}{l}x = 3\sin t + 4\\y = 3\cos t - 3\end{array} \right.$
$ \Rightarrow {x^2} + {y^2} = {\left( {3\sin t + 4} \right)^2} + {\left( {3\cos t - 3} \right)^2} $
$= 9{\sin ^2}t + 9{\cos ^2}t + 24\sin t - 18\cos t + 25 = 24\sin t - 18\cos t + 34$
Mà $24\sin t - 18\cos t \le \sqrt {\left( {{{24}^2} + {{18}^2}} \right)\left( {{{\sin }^2}t + {{\cos }^2}t} \right)} = 30$ (theo bunhiacopxki)
$ \Rightarrow {x^2} + {y^2} \le 30 + 34 = 64 \Rightarrow \sqrt {{x^2} + {y^2}} \le 8 \Rightarrow \left| z \right| \le 8$
Trong các số phức z thỏa mãn \(\left| {z + 3 + 4i} \right| = 2\) , gọi \({z_0}\) là số phức có mô đun nhỏ nhất. Khi đó:
Giả sử $z = a + bi\left( {a,b \in R} \right)$ ta có:
$\left| {z + 3 + 4i} \right| = 2 \Leftrightarrow \left| {(a + 3) + (b + 4)i} \right| = 2 \Leftrightarrow {(a + 3)^2} + {(b + 4)^2} = 4$
Do đó tập hợp điểm biểu diễn số phức $z$ thuộc đường tròn tâm $I\left( { - 3; - 4} \right)$ và bán kính $r = 2$
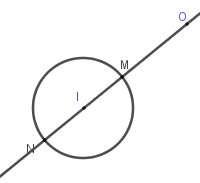
Từ hình vẽ ta thấy số phức \({z_0}\) có mô đun nhỏ nhất nếu \({z_0}\) có điểm biểu diễn là \(M\).
Ta có: $\overrightarrow {OI} = ( - 3; - 4)$ nên đường thẳng đi qua \(O\) và \(I\) là $OI:\left\{ \begin{array}{l}x = 3t\\y = 4t\end{array} \right. \Rightarrow M\left( {3t;4t} \right)$
Mặt khác $M \in \left( C \right)$ nên: ${\left( {3t + 3} \right)^2} + {\left( {4t + 4} \right)^2} = 4 \Leftrightarrow 25{t^2} + 50t + 21 = 0 \Leftrightarrow \left\{ \begin{array}{l}t = \dfrac{{ - 3}}{5}\\t = \dfrac{{ - 7}}{5}\end{array} \right.$
$M\left( {\dfrac{{ - 9}}{5};\dfrac{{ - 12}}{5}} \right)$ hoặc $M\left( {\dfrac{{ - 21}}{5};\dfrac{{ - 28}}{5}} \right)$
$M\left( {\dfrac{{ - 9}}{5};\dfrac{{ - 12}}{5}} \right)$ thuộc $\left( C \right)$ và gần $O$ nhất.
$ \Rightarrow z = \dfrac{{ - 9}}{5} - \dfrac{{12}}{5}i \Rightarrow \left| z \right| = 3$
Xét các số phức \(z,\,\,w\) thỏa mãn \(\left| z \right| = 2,\,\,\left| {iw - 2 + 5i} \right| = 1\). Giá trị nhỏ nhất của \(\left| {{z^2} - wz - 4} \right|\) bằng:
Theo bài ra ta có :
+) \(\left| z \right| = 2 \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(z\) là đường tròn tâm \({I_1}\left( {0;0} \right)\) bán kính \({R_1} = 2\).
\(\left| i \right|\left| {w - \dfrac{{2 - 5i}}{i}} \right| = 1 \Leftrightarrow \left| {w - \left( { - 5 - 2i} \right)} \right| = 1\)
\( \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(w\) là đường tròn tâm \({I_2}\left( { - 5; - 2} \right)\) bán kính \({R_2} = 1\).
Đặt \(T = \left| {{z^2} - wz - 4} \right| = \left| {{z^2} - wz - z.\overline z } \right| = \left| z \right|\left| {z - w - \overline z } \right| = 2\left| {z - w - \overline z } \right|\)
Đặt \(z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi \Rightarrow z - \overline z = 2bi\).
\( \Rightarrow T = 2\left| {2bi - w} \right|\).
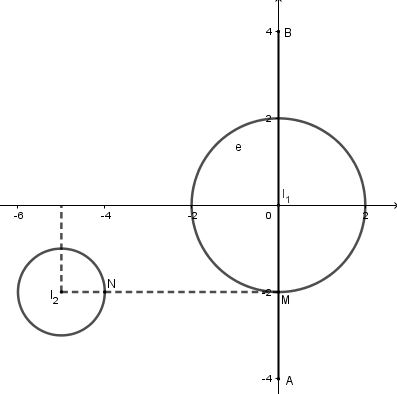
Gọi \(M\left( {0;2b} \right)\) là điểm biểu diễn số phức \(2bi\), \(N\) là điểm biểu diễn số phức \(w\).
\( \Rightarrow T = 2M{N_{\min }} \Leftrightarrow M{N_{\min }}\).
Do \(\left| z \right| = 2 \Rightarrow {a^2} + {b^2} = 4 \Leftrightarrow - 2 \le b \le 2 \Leftrightarrow - 4 \le 2b \le 4\).
\( \Rightarrow \) Tập hợp các điểm \(M\) là đoạn \(AB\) với \(A\left( { 0;-4} \right),\,\,B\left( {0;4} \right)\).
Dựa vào hình vẽ ta thấy \(M{N_{\min }} = 4 \Leftrightarrow N\left( { - 4; - 2} \right),M\left( {0; - 2} \right)\).
Vậy \({T_{\min }} = 2.4 = 8\).
Đề thi THPT QG - 2021 - mã 101
Xét các số phức \(z,\,{\rm{w}}\) thỏa mãn \(\left| z \right| = 1\) và \(\left| {\rm{w}} \right| = 2.\) Khi \(\left| {z + i\,\overline {\rm{w}} - 6 - 8i} \right|\) đạt giá trị nhỏ nhất, \(\left| {z - {\rm{w}}} \right|\) bằng?
Cách 1: Dùng phương pháp hình học \( \to \) Kỹ năng dồn số phức.
* \(P = \left| {z + i\,\overline {\rm{w}} - 6 - 8i} \right| = \left| {\left( {z - 6 - 8i} \right) - \left( { - i\overline w } \right)} \right| = \left| {u - v} \right|\).
Trong đó: \(\left\{ \begin{array}{l}u = z - 6 - 8i\\v = - i\overline w \end{array} \right.\), \(u\) có điểm biểu diễn là \(A\), \(v\) có điểm biểu diễn là \(B\).
\( \Rightarrow P = \left| {u - v} \right| = AB \Rightarrow \) Cần đạt Min.
* \(\left| z \right| = 1 \Leftrightarrow \left| {\left( {z - 6 - 8i} \right) + 6 + 8i} \right| = 1 \Leftrightarrow \left| {u + 6 + 8i} \right| = 1\).
\( \Rightarrow \) Tập hợp điểm \(A\) biểu diễn số phức \(u\) là đường tròn: \(\left( {{C_1}} \right)\): \(\left\{ \begin{array}{l}I\left( { - 6; - 8} \right)\\{R_1} = 1\end{array} \right.\).
* \(\left| w \right| = 2 \Leftrightarrow \left| {\overline w } \right| = 2 \Leftrightarrow \left| { - i} \right|.\left| {\overline w } \right| = \left| { - i} \right|.2\) \( \Rightarrow \left| { - i\overline w } \right| = 2 \Leftrightarrow \left| v \right| = 2\).
\( \Rightarrow \) Tập hợp điểm \(B\) biểu diễn số phức \(v\) là đường tròn \(\left( {{C_2}} \right):\,\,\left\{ \begin{array}{l}O\left( {0;0} \right)\\{R_2} = 2\end{array} \right.\).
Có \(\left\{ \begin{array}{l}IA = {R_1} = 1\\OB = {R_2} = 2\\OI = 10\end{array} \right.\)
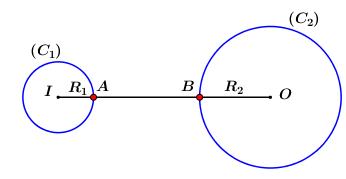
\( \Rightarrow A{B_{\min }} = IO - {R_1} - {R_2} = 10 - 1 - 2 = 7\).
Min đạt được khi: \(\left\{ \begin{array}{l}\overrightarrow {OA} = \dfrac{9}{{10}}\overrightarrow {OI} \Rightarrow A\left( {\dfrac{{ - 27}}{5};\dfrac{{ - 36}}{5}} \right) \Rightarrow u = - \dfrac{{27}}{5} - \dfrac{{36}}{5}i\\\overrightarrow {OB} = \dfrac{1}{5}\overrightarrow {OI} \Rightarrow B\left( {\dfrac{{ - 6}}{5};\dfrac{{ - 8}}{5}} \right) \Rightarrow v = - \dfrac{6}{5} - \dfrac{8}{5}i\end{array} \right.\).
\( \Rightarrow \left\{ \begin{array}{l}z = u + 6 + 8i = \dfrac{3}{5} + \dfrac{4}{5}i\\ - i\overline w = v \Rightarrow \overline w = \dfrac{v}{{ - i}} = \dfrac{{ - \dfrac{6}{5} - \dfrac{8}{5}i}}{{ - i}} = \dfrac{8}{5} - \dfrac{6}{5}i \Rightarrow w = \dfrac{8}{5} + \dfrac{6}{5}i\end{array} \right.\)
\( \Rightarrow \left| {z - w} \right| = \left| {\left( {\dfrac{3}{5} + \dfrac{4}{5}i} \right) - \left( {\dfrac{8}{5} + \dfrac{6}{5}i} \right)} \right| = \dfrac{{\sqrt {29} }}{5}\).
Cách 2: Phương pháp dùng BĐT vectơ
Ta có BĐT cho 3 vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) thì \(\left| {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right| \ge \left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| - \left| {\overrightarrow c } \right|\).
Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}\left| {\overrightarrow a } \right| \ge \left| {\overrightarrow b } \right| + \left| {\overrightarrow c } \right|\\\overrightarrow a = k\overrightarrow b \\\overrightarrow a = m\overrightarrow c \end{array} \right.\,\,\left( {k;m < 0} \right)\).
* Đặt \(P = \left| {z + i\,\overline {\rm{w}} - 6 - 8i} \right| = \left| {\underbrace {\left( { - 6 - 8i} \right)}_{ = \overrightarrow a } + \underbrace z_{ = \overrightarrow b } + \underbrace {i\overline w }_{ = \overrightarrow c }} \right|\)
Đặt \(\left\{ \begin{array}{l}\left( { - 6 - 8i} \right) \Leftrightarrow \overrightarrow a \left( { - 6; - 8} \right) \Rightarrow \left| {\overrightarrow a } \right| = 10\\z \Leftrightarrow \overrightarrow b \Rightarrow \left| {\overrightarrow b } \right| = 1\\i\overline w \Leftrightarrow \overrightarrow c \Rightarrow \left| {\overrightarrow c } \right| = \left| {i\overline w } \right| = \left| w \right| = 2\end{array} \right.\).
\( \Rightarrow P = \left| {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right| \ge \left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| - \left| {\overrightarrow c } \right| = 10 - 1 - 2 = 7\).
\( \Rightarrow {P_{\min }} = 7\), đạt Min khi \(\left\{ \begin{array}{l}\left| {\overrightarrow a } \right| \ge \left| {\overrightarrow b } \right| + \left| {\overrightarrow c } \right|\,\,\left( {dung\,\,do\,\,10 > 1 + 2} \right)\\\overrightarrow a = - 10\overrightarrow b \Leftrightarrow \overrightarrow b = - \dfrac{1}{{10}}\overrightarrow a = \left( {\dfrac{3}{5};\dfrac{4}{5}} \right)\\\overrightarrow a = - 5\overrightarrow c \Leftrightarrow \overrightarrow c = - \dfrac{1}{5}\overrightarrow a = \left( {\dfrac{6}{5};\dfrac{8}{5}} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}z = \dfrac{3}{5} + \dfrac{4}{5}i\\i\overline w = \dfrac{6}{5} + \dfrac{8}{5}i \Leftrightarrow w = \dfrac{8}{5} + \dfrac{6}{5}i\end{array} \right.\)
\( \Rightarrow \left| {z - w} \right| = \left| {\left( {\dfrac{3}{5} + \dfrac{4}{5}i} \right) - \left( {\dfrac{8}{5} + \dfrac{6}{5}i} \right)} \right| = \dfrac{{\sqrt {29} }}{5}\).
Xét các số phức \(z\) thỏa mãn \(|z - 2| = |z - 2i|\). Môđun nhỏ nhất của số phức \(w = z + 4 - 2i\) bằng
Đặt \(z = a + bi\)
Ta có:
\(\left| {z - 2} \right| = |z - 2i| \)\(\Rightarrow |(a - 2) + bi| = |a + (b - 2)i|\)
\( \Rightarrow \quad {(a - 2)^2} + {b^2} = {a^2} + {(b - 2)^2}\)
\( \Rightarrow - 4a + 4 = - 4b + 4 \Leftrightarrow a = b.\)
\( \Rightarrow w = a + bi + 4 - 2i = a + 4 + (a - 2)i\)
\( \Rightarrow |w| = \sqrt {{{(a + 4)}^2} + {{(a - 2)}^2}} = \sqrt {2{a^2} + 4a + 20} \ge \sqrt {18} \)
\( \Rightarrow |w{|_{\min }} = 3\sqrt 2 {\rm{ }}\) tại \(a = - 1\).

