Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy là hình vuông, \(SA\) vuông góc với đáy. Hình chóp có bao nhiêu mặt bên là tam giác vuông?
Trả lời bởi giáo viên
Đáp án đúng: d
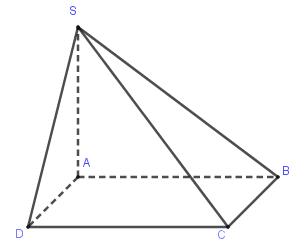
Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AD,SA \bot AB \Rightarrow \Delta SAB,\Delta SAD\) vuông tại \(A\).
Lại có \(CD \bot SA,CD \bot AD \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD \Rightarrow \Delta SCD\) vuông tại $D.$
\(CB \bot SA,CB \bot AB \Rightarrow CB \bot \left( {SAB} \right) \Rightarrow CB \bot SB \Rightarrow \Delta SCB\) vuông tại \(B\).
Vậy có tất cả $4$ mặt là các tam giác vuông.
Hướng dẫn giải:
Dựng hình và tìm các tam giác vuông trong số bốn mặt bên của hình chóp.
Sử dụng định lý: “Đường thẳng vuông góc với hai đường thẳng cắt nhau thì nó vuông góc với mặt phẳng chứa hai đường thẳng đó”
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
