Đáp án: Trải hình chóp SABCD trên cùng một mặt phẳng ( left( {{A_1} equiv A} right) ) Giả sử quãng đường của con kiến đi từ A đến A1 là AA’B’C’A1 , khi đó quãng đường con kiến đi ngắn nhất là độ dài đoạn AA1...

Trải hình chóp SABCD trên cùng một mặt phẳng ( left( {{A_1} equiv A} right) ) Giả sử quãng đường của con kiến đi từ A đến A1 là AA’B’C’A1 , khi đó quãng đường con kiến đi ngắn nhất là độ dài đoạn AA1...

Câu hỏi:

2 năm trước

Có một mô hình kim tự tháp là một chóp tứ giác đều có cạnh bằng 6cm; cạnh đáy bằng 4cm được đặt trên một bàn trưng bày (đáy nằm trên mặt bàn). Một chú kiến tinh nghịch đang ở đỉnh của đáy và có ý định khám phá một vòng qua tất cả các mặt và trở về vị trí ban đầu. Tính quãng đường ngắn nhất của chú kiến (nếu kết quả lẻ thì làm tròn đến 2 chữ số thập phân).

Đáp án:
$cm$

Xem đáp án

74 lượt xem

Khái niệm về khối đa diện - MÔN TOÁN - Lớp 12. Thi ngay

Trả lời bởi giáo viên

Đáp án:

Đáp án:

$cm$

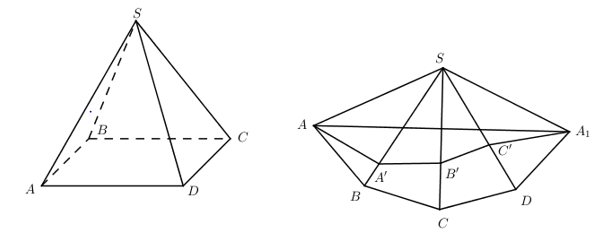
Trải hình chóp S.ABCD trên cùng một mặt phẳng $\left( {{A_1} \equiv A} \right)$.

Giả sử quãng đường của con kiến đi từ A đến A₁ là AA’B’C’A₁ , khi đó quãng đường con kiến đi ngắn nhất là độ dài đoạn AA₁.

Xét tam giác SAB có:

$\begin{array}{l}\cos \angle ASB = \dfrac{{S{A^2} + S{B^2} - A{B^2}}}{{2SA.SB}} = \dfrac{{{6^2} + {6^2} - {4^2}}}{{{{2.6}^2}}} = \dfrac{7}{9}\\ \Rightarrow \angle ASB \approx 38,{9^0}\\ \Rightarrow \angle AS{A_1} = 4\angle ASB \approx 155,{8^0}\end{array}$

Xét tam giác ASA₁ có :

$A{A_1}^2 = S{A^2} + SA_1^2 - 2SA.S{A_1}.\cos \angle AS{A_1} \approx 11,73\,\,\left( {cm} \right)$