Cho lăng trụ tam giác đều $ABC.A’B’C’.$ Trên $A’B'$ kéo dài lấy điểm $M$ sao cho \(B'M = \dfrac{1}{2}A'B'\). Gọi $N, P$ lần lượt là trung điểm của $A’C’$ và $B’B.$ Mặt phẳng $(MNP)$ chia khối lăng trụ $ABC.A’B’C’ $ thành hai khối đa diện trong đó khối đa diện chứa đỉnh $A’$ có thể tích \({V_1}\) và khối đa diện chứa đỉnh $C’$ có thể tích \({V_2}\). Tính \(\dfrac{{{V_1}}}{{{V_2}}}\).

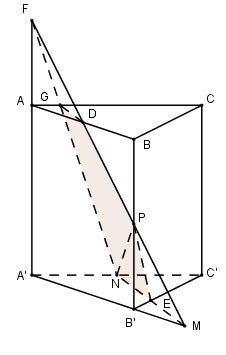
Gọi \(E = MN \cap B'C'\)

Kéo dài $MP$ cắt $AB$ tại $D,$ cắt $AA'$ tại $F.$

Nối $NF,$ cắt $AC$ tại $G.$

Do đó thiết diện của lăng trụ khi cắt bởi mặt phẳng $(MNP)$ là $NEPDG.$

Gọi \({V_1}\) là thể tích khối đa diện chứa đỉnh $A’$ ta có :

\({V_1} = {V_{F.A'MN}} - {V_{F.ADG}} - {V_{P.B'EM}}\)

Ta có:

\({S_{A'MN}} = \dfrac{1}{2}d\left( {N;A'M} \right).A'M = \dfrac{1}{2}.\dfrac{1}{2}d\left( {C';A'B'} \right).\dfrac{3}{2}A'B' = \dfrac{3}{4}{S_{A'B'C'}}\)

\(\Delta BDP = \Delta B'MP \Rightarrow BD = B'M = \dfrac{1}{2}AB \Rightarrow D\) là trung điểm của AB.

\( \Rightarrow \dfrac{{FA}}{{FA'}} = \dfrac{{AD}}{{A'M}} = \dfrac{1}{3} \Rightarrow \dfrac{{FA'}}{{AA'}} = \dfrac{3}{2}\)

\( \Rightarrow \dfrac{{{V_{F.A'MN}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{\dfrac{1}{3}.FA'.{S_{A'MN}}}}{{AA'.{S_{ABC}}}} = \dfrac{1}{3}.\dfrac{3}{2}.\dfrac{3}{4} = \dfrac{3}{8} \Rightarrow {V_{F.A'MN}} = \dfrac{3}{8}{V_{ABC.A'B'C'}} = \dfrac{{3V}}{8}\)

Dễ dàng chứng minh được \(\Delta ADG\) đồng dạng \(\Delta A'MN\) theo tỉ số \(\dfrac{1}{3} \Rightarrow {S_{ADG}} = \dfrac{1}{9}{S_{A'MN}} = \dfrac{1}{{12}}{S_{A'B'C'}}\)

\( \Rightarrow \dfrac{{{V_{F.ADG}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{\dfrac{1}{3}.FA.{S_{ADG}}}}{{AA'.{S_{A'B'C'}}}} = \dfrac{1}{3}.\dfrac{1}{2}.\dfrac{1}{{12}} = \dfrac{1}{{72}} \Rightarrow {V_{F.ADG}} = \dfrac{1}{{72}}{V_{ABC.A'B'C'}} = \dfrac{V}{{72}}\) 

Áp dụng định lí Menelaus trong tam giác $A’B’C’$ ta có :

\(\dfrac{{MA'}}{{MB'}}.\dfrac{{EB'}}{{EC'}}.\dfrac{{NC'}}{{NA'}} = 1 \Leftrightarrow 3.\dfrac{{EB'}}{{EC'}}.1 = 1 \Leftrightarrow \dfrac{{EB'}}{{EC'}} = \dfrac{1}{3}\)

Áp dụng định lí Menelaus trong tam giác $A’MN$ ta có :

\(\dfrac{{C'N}}{{C'A'}}.\dfrac{{B'A'}}{{B'M}}.\dfrac{{EM}}{{EN}} = 1 \Leftrightarrow \dfrac{1}{2}.2.\dfrac{{EM}}{{EN}} = 1 \Leftrightarrow \dfrac{{EM}}{{EN}} \Rightarrow \dfrac{{ME}}{{MN}} = \dfrac{1}{2}\)

\( \Rightarrow \dfrac{{{S_{B'EM}}}}{{{S_{A'NM}}}} = \dfrac{{MB'}}{{MA'}}.\dfrac{{ME}}{{MN}} = \dfrac{1}{3}.\dfrac{1}{2} = \dfrac{1}{6} \Rightarrow {S_{B'EM}} = \dfrac{1}{6}{S_{A'NM}} = \dfrac{1}{8}{S_{A'B'C'}}\)

\( \Rightarrow \dfrac{{{V_{P.B'EM}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{\dfrac{1}{3}.PB'.{S_{B'EM}}}}{{BB'.{S_{A'B'C'}}}} = \dfrac{1}{3}.\dfrac{1}{2}.\dfrac{1}{8} = \dfrac{1}{{48}} \Rightarrow {V_{P.B'EM}} = \dfrac{1}{{48}}V\)

Vậy  \({V_1} = \dfrac{{49}}{{144}}V \Rightarrow {V_2} = \dfrac{{95}}{{144}}V \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{49}}{{95}}\)