Cho khối lăng trụ \(ABC.A'B'C',\) khoảng cách từ \(C\) đến đường thẳng \(BB'\) bằng \(\sqrt 5 ,\) khoảng cách từ \(A\) đến các đường thẳng \(BB'\) và \(CC'\) lần lượt bằng \(1\) và \(2,\) hình chiếu vuông góc của \(A\) lên mặt phẳng \(\left( {A'B'C'} \right)\) là trung điểm \(M\) của \(B'C'\) và \(A'M = \sqrt 5 .\) Thể tích của khối lăng trụ đã cho bằng:

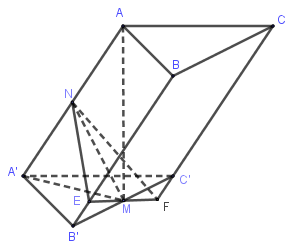
Qua \(M\) dựng mặt phẳng \(\left( P \right)\) vuông góc với \(AA'\) cắt các cạnh \(AA',\;BB',\;CC'\) lần lượt tại \(N,\;E,\;F.\)

Ta có: \(\left\{ \begin{array}{l}AA' \bot NE \Rightarrow NE = d\left( {E,\;AA'} \right) = d\left( {N,\;BB'} \right) = d\left( {A,\;BB'} \right) = 1.\\AA' \bot NF \Rightarrow NF = d\left( {F,\;AA'} \right) = d\left( {N,\;CC'} \right) = d\left( {A,\;CC'} \right) = 2\\AA' \bot \left( P \right) \Rightarrow CC' \bot \left( P \right) \Rightarrow CC' \bot EF \Rightarrow EF = d\left( {E,\;CC'} \right) = d\left( {F,\;BB'} \right) = d\left( {C,\;BB'} \right) = \sqrt 5 .\end{array} \right.\)

Có: \(N{E^2} + N{F^2} = EF{'^2} \Rightarrow \Delta NEF\) vuông tại \(N.\)  (định lý Pi-ta-go đảo)

Mà: \(\dfrac{{ME}}{{MF}} = \dfrac{{MB'}}{{MC'}} = 1 \Rightarrow ME = MF\) (định lý Ta-lét)\( \Rightarrow M\) là trung điểm của \(EF.\)

\( \Rightarrow MN = \dfrac{1}{2}EF = \dfrac{{\sqrt 5 }}{2}.\)

Xét tam giác \(AA'M\) vuông tại \(M\) ta có:

\(\dfrac{1}{{M{N^2}}} = \dfrac{1}{{A{M^2}}} + \dfrac{1}{{A'{M^2}}} \Leftrightarrow \dfrac{4}{5} = \dfrac{1}{{A{M^2}}} + \dfrac{1}{5} \Leftrightarrow AM = \dfrac{{\sqrt {15} }}{3}.\)

Ta có: \(\left\{ \begin{array}{l}\left( P \right) \bot AA'\\\left( {A'B'C'} \right) \bot AM\end{array} \right.\)\( \Rightarrow \widehat {\left( {\left( P \right),\;\left( {A'B'C'} \right)} \right)} = \widehat {\left( {AA',\;AM} \right)} = \widehat {A'MA}\)

\( \Rightarrow \cos \widehat {A'AM} = \dfrac{{AM}}{{AA'}} = \dfrac{{\dfrac{{\sqrt {15} }}{3}}}{{\sqrt {5 + \dfrac{5}{3}} }} = \dfrac{1}{2}.\)

Ta thấy \(\Delta NEF\) là hình chiếu vuông góc của \(\Delta A'B'C'\) lên mặt phẳng \(\left( P \right).\)

\(\begin{array}{l} \Rightarrow {S_{A'B'C'}} = \dfrac{{{S_{NEF}}}}{{\cos \widehat {A'AM}}} = \dfrac{{\dfrac{1}{2}NE.NF}}{{\dfrac{1}{2}}} = 1.2 = 2.\\ \Rightarrow {V_{ABC.A'B'C'}} = {S_{A'B'C'}}.AM = 2.\dfrac{{\sqrt {15} }}{3} = \dfrac{{2\sqrt {15} }}{3}.\end{array}\)