Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là $a,\,\,2a,\,\,3a$ có thể tích lớn nhất bằng
Trả lời bởi giáo viên
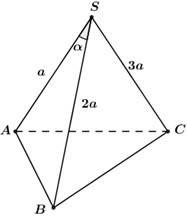
Xét khối chóp tam giác $S.ABC,$ có $\left\{ \begin{array}{l}SA = a,\,\,SB = 2a\\SC = 3a,\,\,\widehat {ASB} = \alpha \end{array} \right.$ và $h$ là khoảng cách từ $C$ đến $(SAB)$
Khi đó, thể tích khối chóp $S.ABC$ là $V = \dfrac{1}{3}.d\left( {C;\left( {SAB} \right)} \right).{S_{\Delta \,SAB}}$ $\left( 1 \right).$
Diện tích tam giác $SAB$ là ${S_{\Delta \,SAB}} = \dfrac{1}{2}.SA.SB.\sin \widehat {ASB} = {a^2}.\sin \alpha $ $\left( 2 \right).$
Từ $\left( 1 \right),\,\,\left( 2 \right)$ suy ra $V = \dfrac{1}{3}.h.{a^2}.\sin \alpha $ mà $\left\{ \begin{array}{l}\sin \alpha \le 1\\h \le SC = 3a\end{array} \right.$$ \Rightarrow V \le \dfrac{1}{3}.3a.{a^2} = {a^3}.$
Dấu "=" xảy ra khi $\sin \alpha =1$ và $h=SC=3a$ hay hình chóp $S.ABC$ là tứ diện vuông đỉnh $S$.
Hướng dẫn giải:
Xác định khoảng cách, biện luận góc và vị trí điểm để tìm GTLN của thể tích.

