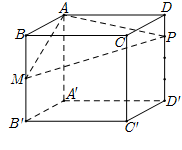
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(2a,\) gọi \(M\) là trung điểm của $BB'$ và \(P\) thuộc cạnh $DD'$ sao cho $DP\, = \,\dfrac{1}{4}DD'.$ Mặt phẳng $(AMP)$ cắt $CC'$ tại$N.$ Thể tích khối đa diện $AMNPBCD$ bằng

Cho tứ diện $ABCD $ và $G$ là trọng tâm tam giác $ACD.$ Mặt phẳng $(P)$ qua $BG$ và song song với $CD$ chia khối tứ diện thành hai phần. Tính tỉ số thể tích (số bé chia số lớn) của hai phần đó là:

Cho hình chóp $S.ABC$ có $AB = 5cm,\;BC = 6cm,\;CA = 7cm$. Hình chiếu vuông góc của $S$ xuống mặt phẳng $\left( {ABC} \right)$ nằm bên trong tam giác $ABC$. Các mặt phẳng $\left( {SAB} \right),\left( {SBC} \right),\left( {SCA} \right)$ đều tạo với đáy một góc $60^\circ $. Gọi $AD,\;BE,\;CF$ là các đường phân giác của tam giác $ABC$ với $D \in BC,E \in AC,F \in AB$ .Thể tích $S.DEF$ gần nhất với số nào sau đây? 

Khối chóp $S.ABCD$ có đáy là hình thoi cạnh $a,$ $SA = SB = SC = a$, cạnh $SD$ thay đổi. Thể tích khối chóp $S.ABCD$ lớn nhất khi độ dài cạnh $SD$ là:

Cho khối lăng trụ \(ABC.A'B'C',\) khoảng cách từ \(C\) đến đường thẳng \(BB'\) bằng \(\sqrt 5 ,\) khoảng cách từ \(A\) đến các đường thẳng \(BB'\) và \(CC'\) lần lượt bằng \(1\) và \(2,\) hình chiếu vuông góc của \(A\) lên mặt phẳng \(\left( {A'B'C'} \right)\) là trung điểm \(M\) của \(B'C'\) và \(A'M = \sqrt 5 .\) Thể tích của khối lăng trụ đã cho bằng:

Cho tứ diện đều $ABCD $ có cạnh bằng $3.$ Gọi $M, N$ là hai điểm thay đổi lần lượt thuộc cạnh $BC, BD$ sao cho mặt phẳng $(AMN)$ luôn vuông góc với mặt phẳng $(BCD).$ Gọi $V_1, V_2$ lần lượt là giá trị lớn nhất và nhỏ nhất của thể tích khối tứ diện $ABMN.$ Tính $V_1 +V_2$?

Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là $a,\,\,2a,\,\,3a$ có thể tích lớn nhất bằng

Cho lăng trụ tam giác đều $ABC.A’B’C’.$ Trên $A’B'$ kéo dài lấy điểm $M$ sao cho \(B'M = \dfrac{1}{2}A'B'\). Gọi $N, P$ lần lượt là trung điểm của $A’C’$ và $B’B.$ Mặt phẳng $(MNP)$ chia khối lăng trụ $ABC.A’B’C’ $ thành hai khối đa diện trong đó khối đa diện chứa đỉnh $A’$ có thể tích \({V_1}\) và khối đa diện chứa đỉnh $C’$ có thể tích \({V_2}\). Tính \(\dfrac{{{V_1}}}{{{V_2}}}\).