Câu hỏi:
2 năm trước
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy ABC là tam giác vuông, AB=BC=a. Biết rằng góc giữa hai mặt phẳng (ACC′) và (AB′C′) bằng 600 (tham khảo hình vẽ bên). Thể tích của khối chóp B′.ACC′A′ bằng
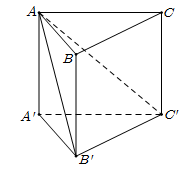
Trả lời bởi giáo viên
Đáp án đúng: a
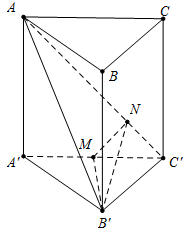
Dựng B′M⊥A′C′⇒B′M⊥(ACC′A′)
Dựng MN⊥AC′⇒AC′⊥(MNB′)
Khi đó ^((AB′C′);(AC′A′))=^MNB′=600
Ta có: B′M=a√22⇒MN=B′Mtan^MNB′=a√66
Mặt khác tan^AC′A′=MNC′N=AA′A′C′
Trong đó MN=a√66;MC′=a√22⇒C′N=√C′M2−MN2=a√33
Suy ra AA′=a
Thể tích lăng trụ V=AB22.AA′=a32⇒VB′.ACC′A′=V−VB′.BAC=V−V3=23V=a33.
Hướng dẫn giải:
VB′.ACC′A′=V−VB′.BAC=23V, với V là thể tích khối lăng trụ.
Tính thể tích khối lăng trụ.

