Câu hỏi:
2 năm trước
Cho hình chóp đều $S.ABCD $ có đáy là hình vuông cạnh $a,$ $M$ là trung điểm của $SA.$ Biết mặt phẳng $(MCD)$ vuông góc với mặt phẳng $(SAB).$ Thể tích khối chóp $S.ABCD$ là:
Trả lời bởi giáo viên
Đáp án đúng: d
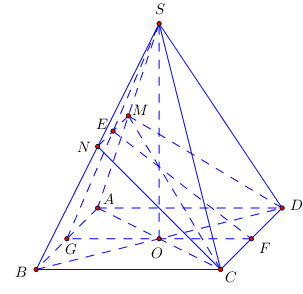
Gọi $N$ là trung điểm của $SB$ ta có \(\left( {MCD} \right) \equiv \left( {MNCD} \right)\).
\( \Rightarrow \left( {MNCD} \right) \bot \left( {SAB} \right)\)
Dễ thấy \(\Delta BCN = \Delta ADM\,\,\left( {c.g.c} \right) \Rightarrow CN = DM\)
\( \Rightarrow MNCD\) là hình thang cân. Gọi $E, F$ lần lượt là trung điểm của $MN$ và $CD$ ta có \(EF \bot MN\)
\( \Rightarrow EF \bot \left( {SAB} \right)\)
Gọi $G$ là trung điểm $AB$ ta có $S, E, G$ thẳng hàng.
Đặt \(SA = SB = SC = SD = x\) ta có \(CN = \dfrac{{\sqrt {{x^2} + 2{a^2}} }}{2}\)
Dễ dàng tính được \(EF = \dfrac{{\sqrt {4{x^2} + 7{a^2}} }}{4}\)
Ta có \(EG = \dfrac{1}{2}SG = \dfrac{1}{2}\sqrt {{x^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{\sqrt {4{x^2} - {a^2}} }}{4}\)
\(\Delta EFG\) vuông tại $E$ \( \Rightarrow E{F^2} + E{G^2} = G{F^2} \Leftrightarrow \dfrac{{4{x^2} + 7{a^2}}}{{16}} + \dfrac{{4{x^2} - {a^2}}}{{16}} = {a^2}\)
\( \Leftrightarrow 4{x^2} + 7{a^2} + 4{x^2} - {a^2} = 16{a^2} \Leftrightarrow 8{x^2} = 10{a^2} \Leftrightarrow {x^2} = \dfrac{{5{a^2}}}{4}\)
Xét tam giác vuông $SOB:$ \(SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {\dfrac{{5{a^2}}}{4} - \dfrac{{{a^2}}}{2}} = \dfrac{{\sqrt 3 a}}{2}\)
Vậy thể tích khối chóp là \({V_{S.ABCD}} = \dfrac{1}{3}.SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{\sqrt 3 a}}{2}.{a^2} = \dfrac{{\sqrt 3 {a^3}}}{6}\)
Hướng dẫn giải:
Gọi $O$ là tâm mặt đáy \( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}\).
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
