Cho hàm số $y = f\left( x \right)$ có đồ thị như hình bên. Giá trị lớn nhất của hàm số này trên đoạn $\left[ { - 2;3} \right]$ bằng:

Nhận thấy trên đoạn $\left[ { - 2;3} \right]$ đồ thị hàm số có điểm cao nhất có tọa độ $\left( {3;4} \right).$
\( \Rightarrow \) giá trị lớn nhất của hàm số này trên đoạn $\left[ { - 2;3} \right]$ bằng \(4.\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên sau:
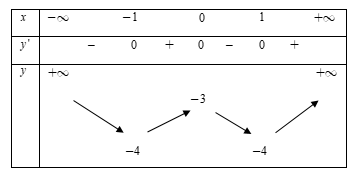
Khẳng định nào sau đây là đúng?
A sai vì hàm số có ba điểm cực trị là \(x = - 1;{\rm{ }}x = 0;{\rm{ }}x = 1.\)
C sai vì hàm số không có giá trị lớn nhất.
D sai vì hàm số có hai điểm cực tiểu là \(x = - 1\) và \(x = 1.\)
Tìm giá trị lớn nhất của hàm số $y = {x^4} - 2{x^2} - 15$ trên đoạn $\left[ { - 3;{\mkern 1mu} {\mkern 1mu} 2} \right]$.
Ta có: $y' = 4{x^3} - 4x \Rightarrow y' = 0 \Leftrightarrow 4x\left( {{x^2} - 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0{\mkern 1mu} {\mkern 1mu} \in \left[ { - 3;{\mkern 1mu} {\mkern 1mu} 2} \right]}\\{x = 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \in \left[ { - 3;{\mkern 1mu} {\mkern 1mu} 2} \right]}\\{x = {\rm{\;}} - 1{\mkern 1mu} {\mkern 1mu} \in \left[ { - 3;{\mkern 1mu} {\mkern 1mu} 2} \right]}\end{array}} \right.$
$ \Rightarrow f\left( { - 3} \right) = 48;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} f\left[ { - 1} \right) = {\rm{\;}} - 16;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} f\left( 0 \right) = {\rm{\;}} - 15;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} f\left( 1 \right) = {\rm{\;}} - 16;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} f\left( 2 \right) = {\rm{\;}} - 7.$
Như vậy $\mathop {\max }\limits_{\left[ { - 3;{\kern 1pt} {\kern 1pt} 2} \right]} y = 48$.
Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = {x^3} - 3{x^2} - 9x + 35$ trên đoạn $\left[ { - {\mkern 1mu} 4;4} \right].$ Giá trị của $M$ và $m$ lần lượt là
Xét hàm số $y = {x^3} - 3{x^2} - 9x + 35$ trên đoạn $\left[ { - {\mkern 1mu} 4;4} \right],$ có $y' = 3{x^2} - 6x - 9.$
Phương trình $y' = 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - {\mkern 1mu} 4 \le x \le 4}\\{3{x^2} - 6x - 9 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - {\mkern 1mu} 1}\\{x = 3}\end{array}} \right..$
Tính các giá trị$f\left( { - {\mkern 1mu} 4} \right) = - {\mkern 1mu} 41;{\mkern 1mu} {\mkern 1mu} f\left( { - {\mkern 1mu} 1} \right) = 40;{\mkern 1mu} {\mkern 1mu} f\left( 3 \right) = 8;{\mkern 1mu} {\mkern 1mu} f\left( 4 \right) = 15.$
Vậy giá trị lớn nhất và nhỏ nhất của hàm số lần lượt là $M = 40;{\mkern 1mu} {\mkern 1mu} m = - {\mkern 1mu} 41.$
Giá trị nhỏ nhất của hàm số $y = 1 + x + \dfrac{4}{x}$ trên đoạn $\left[ { - 3;{\mkern 1mu} {\mkern 1mu} - 1} \right]$ bằng
Hàm số đã xác định và liên tục trên $\left[ { - 3; - 1} \right]$.Ta có :
$y' = 1 - \dfrac{4}{{{x^2}}} \Rightarrow y' = 0 \Leftrightarrow {x^2} = 4 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\rm{\;}}&{x = - 2\;\;\left( { \in \left[ { - 3;\; - 1} \right]} \right)}\\{{\rm{ \;}}}&{x = 2\;\;\left( { \notin \left[ { - 3;\; - 1} \right]} \right)}\end{array}} \right..$
Tính $y\left( { - 3} \right) = - \dfrac{{10}}{3}{\rm{; }}y\left( { - 1} \right) = - 4;{\rm{ }}y\left( { - 2} \right) = - 3 \Rightarrow \mathop {\min }\limits_{\left[ { - 3; - 1} \right]} {\mkern 1mu} y = - 4.$
Ký hiệu $a,{\mkern 1mu} {\mkern 1mu} A$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = \dfrac{{{x^2} + x + 4}}{{x + 1}}$ trên đoạn${\rm{ }}[{\rm{ }}0;{\mkern 1mu} {\mkern 1mu} 2{\rm{ }}]{\rm{ }}.$ Giá trị của $a + A$ bằng
Điều kiện: $x \ne 1.$
Ta có $y = x + \dfrac{4}{{x + 1}} \Rightarrow y' = 1 - \dfrac{4}{{{{\left( {x + 1} \right)}^2}}}{\mkern 1mu} .$
$ \Rightarrow y' = 0 \Leftrightarrow {\left( {x + 1} \right)^2} = 4 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\rm{\;}}&{x = 1 \in \left[ {0;\;2} \right]}\\{{\rm{ \;}}}&{x = 3 \notin \left[ {0;\;2} \right]}\end{array}} \right..$
Tính $y\left( 0 \right) = 4;\;y\left( 2 \right) = \dfrac{{10}}{3};\;y\left( 1 \right) = 3 \Rightarrow {\mkern 1mu} {\mkern 1mu} \left\{ {\begin{array}{*{20}{l}}{\min y = 3}\\{\max y = 4}\end{array}} \right. \Rightarrow {\mkern 1mu} {\mkern 1mu} \left\{ {\begin{array}{*{20}{l}}{a = 3}\\{A = 4}\end{array}} \right. \Rightarrow a + A = 7.$
Tìm giá trị nhỏ nhất của hàm số $y = x + \dfrac{{25}}{{x - 3}}$ trên khoảng $\left( {3; + \infty } \right)$.
\(\begin{array}{*{20}{l}}{y' = 1 - \dfrac{{25}}{{{{\left( {x - 3} \right)}^2}}} = \dfrac{{{{\left( {x - 3} \right)}^2} - 25}}{{{{\left( {x - 3} \right)}^2}}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x - 3 = 5}\\{x - 3 = - 5}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 8 \in \left( {3; + \infty } \right)}\\{x = - 2 \notin \left( {3; + \infty } \right)}\end{array}} \right.}\\{f\left( 8 \right) = 8 + \dfrac{{25}}{5} = 13 \Rightarrow \mathop {\min }\limits_{\left( {3; + \infty } \right)} f\left( x \right) = 13}\end{array}\)
Gọi $m\;$ là giá trị để hàm số $y = \dfrac{{x - {m^2}}}{{x + 8}}$ có giá trị nhỏ nhất trên $\left[ {0;3} \right]$ bằng $ - 2.$ Mệnh đề nào sau đây là đúng?
Ta có: $y = \dfrac{{x - {m^2}}}{{x + 8}},{\mkern 1mu} {\mkern 1mu} x \ne - 8 \Rightarrow y' = \dfrac{{1.8 - 1.\left( { - {m^2}} \right)}}{{{{\left( {x + 8} \right)}^2}}} = \dfrac{{{m^2} + 8}}{{{{\left( {x + 8} \right)}^2}}} > 0,{\mkern 1mu} {\mkern 1mu} \forall x \ne - 8$
$ \Rightarrow $ Hàm số luôn đồng biến trên các khoảng: $\left( { - \infty ; - 8} \right),{\mkern 1mu} {\mkern 1mu} \left( { - 8; + \infty {\rm{\;}}} \right)$
$ \Rightarrow \mathop {\min }\limits_{\left[ {0;3} \right]} {\mkern 1mu} y = y(0) = - \dfrac{{{m^2}}}{8} = - 2 \Rightarrow m = \pm 4$
Suy ra, $\left| m \right| < 5$.
Biết rằng giá trị nhỏ nhất của hàm số $y = mx + \dfrac{{36}}{{x + 1}}$ trên ${\rm{ }}[{\rm{ }}0;{\mkern 1mu} {\mkern 1mu} 3{\rm{ }}]{\rm{ }}$ bằng $20.$ Mệnh đề nào sau đây đúng?
Ta có $y' = m - \dfrac{{36}}{{{{\left( {x + 1} \right)}^2}}};\;{\mkern 1mu} \forall x \in \left[ {0;3} \right]$ và $y\left( 0 \right) = 36;{\mkern 1mu} {\mkern 1mu} \;y\left( 3 \right) = 3m + 9.$
TH1: Hàm số nghịch biến trên đoạn $\left[ {0;3} \right] \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\rm{\;}}&{m \le \dfrac{9}{4}}\\{\rm{\;}}&{\min y = 3m + 9 = 20}\end{array}} \right.\;$ (vô nghiệm).
TH2: Phương trình $y' = m - \dfrac{{36}}{{{{\left( {x + 1} \right)}^2}}}{\mkern 1mu} {\mkern 1mu} \Rightarrow {\mkern 1mu} {\mkern 1mu} y' = 0 \Leftrightarrow x = - 1 + \dfrac{6}{{\sqrt m }}$ với \(m > 0\)
Giá trị nhỏ nhất của hàm số bằng $20{\mkern 1mu} {\mkern 1mu} \Rightarrow {\mkern 1mu} {\mkern 1mu} y\left( { - 1 + \dfrac{6}{{\sqrt m }}} \right) = 20$
$ \Leftrightarrow m\left( { - 1 + \dfrac{6}{{\sqrt m }}} \right) + \dfrac{{36}}{{ - {\mkern 1mu} 1 + \dfrac{6}{{\sqrt m }} + 1}} = 20 \Leftrightarrow - {\mkern 1mu} m + 6\sqrt m + 6\sqrt m = 20 \Leftrightarrow - {\mkern 1mu} m + 12\sqrt m = 20 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\rm{\;}}&{m = 4}\\{\rm{\;}}&{m = 100}\end{array}} \right..$
Với $m = 100$ loại vì $ - {\mkern 1mu} 1 + \dfrac{6}{{\sqrt {100} }} = - \dfrac{2}{5} \notin \left[ {0;3} \right].$
Vậy $m = 4 \in \left( {2;4} \right].$
Cho $x,y$ là hai số thực thoả mãn điều kiện ${x^2} + {y^2} + xy + 4 = 4y + 3x$. Tìm giá trị lớn nhất của biểu thức $P = 3\left( {{x^3} - {y^3}} \right) + 20{x^2} + 2xy + 5{y^2} + 39x$.
Theo giả thiết
${x^2} + {y^2} + xy + 4 = 4y + 3x $
$\Leftrightarrow {y^2} + \left( {x - 4} \right)y + {x^2} - 3x + 4 = 0$
Ta xem đây là phương trình bậc hai ẩn $y$ và khi đó điều kiện có nghiệm là:
$\Delta = {\left( {x - 4} \right)^2} - 4\left( {{x^2} - 3x + 4} \right) \ge 0$
$ \Leftrightarrow {x^2} - 8x + 16 - 4{x^2} + 12x - 16 \ge 0 $
$\Leftrightarrow - 3{x^2} + 4x \ge 0 $
$\Leftrightarrow 0 \le x \le \dfrac{4}{3}$
Từ giả thiết suy ra ${x^2} + {y^2} + xy = 3x + 4y - 4$. Khi đó:
$P = 3\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right) + 20{x^2} + 2xy + 5{y^2} + 39x$
$ = 3\left( {x - y} \right)\left( {3x + 4y - 4} \right) + 20{x^2} + 2xy + 5{y^2} + 39x$
$ = 3\left( {3{x^2} + xy - 4{y^2} - 4x + 4y} \right) + 20{x^2} + 2xy + 5{y^2} + 39x$
$ = 29{x^2} + 5xy - 7{y^2} + 27x + 12y$
$ = \left( {5{x^2} + 5xy + 5{y^2}} \right) + 24{x^2} - 12{y^2} + 27x + 12y$
$ = 5\left( {{x^2} + xy + {y^2}} \right) + 24{x^2} - 12{y^2} + 27x + 12y$
$ = 5\left( {3x + 4y - 4} \right) + 24{x^2} - 12{y^2} + 27x + 12y$
$ = 24{x^2} - 12{y^2} + 42x + 32y - 20$
$ = 2\left( {12{x^2} - 6{y^2} + 21x + 16y} \right) - 20$
Đặt $g\left( y \right) = - 6{y^2} + 16y + 21x + 12{x^2}$ (ta xem $x$ là tham số)
Khi đó $g\left( y \right) \le g\left( {\dfrac{4}{3}} \right) = 12{x^2} + 21x + \dfrac{{32}}{3}$
Do $x \in \left[ {0;\dfrac{4}{3}} \right]$ nên $12{x^2} + 21x + \dfrac{{32}}{3} \le 60$
Suy ra $g\left( y \right) \le 60$. Vậy giá trị lớn nhất của $P$ là $100$ khi $x = y = \dfrac{4}{3}$
Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \dfrac{{{x^2} - 2x + 2}}{{x - 2}}\) trên \(\left[ {3;2 + 2\sqrt 2 } \right]\). Tính \(M - m\).
Ta có : \(y' = \dfrac{{{x^2} - 4x + 2}}{{{{\left( {x - 2} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2 + \sqrt 2 \in \left[ {3;2 + 2\sqrt 2 } \right]\\x = 2 - \sqrt 2 \notin \left[ {3;2 + 2\sqrt 2 } \right]\end{array} \right.\)
\(y\left( 3 \right) = 5,y\left( {2 + \sqrt 2 } \right) = 2 + 2\sqrt 2 ,y\left( {2 + 2\sqrt 2 } \right) = \dfrac{{4 + 5\sqrt 2 }}{2}\)
Vậy \(M = \dfrac{{4 + 5\sqrt 2 }}{2},m = 2 + 2\sqrt 2 \Rightarrow M - m = \dfrac{{\sqrt 2 }}{2}\)
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình dưới. Tìm \(m\) để bất phương trình \(f\left( x \right) \ge \dfrac{{x + 1}}{{x + 2}} + m\) nghiệm đúng với mọi \(x \in \left[ {0;\,\,1} \right].\)
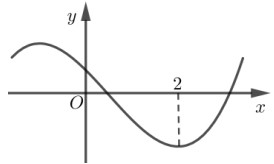
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,f\left( x \right) \ge \dfrac{{x + 1}}{{x + 2}} + m\,\,\,\forall x \in \left[ {0;1} \right]\\ \Leftrightarrow m \le f\left( x \right) - \dfrac{{x + 1}}{{x + 2}} = g\left( x \right)\,\,\forall x \in \left[ {0;1} \right]\\ \Leftrightarrow m \le \mathop {\min }\limits_{\left[ {0;1} \right]} g\left( x \right)\end{array}\)
Xét hàm số \(g\left( x \right) = f\left( x \right) - \dfrac{{x + 1}}{{x + 2}}\) trên \(\left[ {0;1} \right]\) ta có: \(g'\left( x \right) = f'\left( x \right) - \dfrac{1}{{{{\left( {x + 2} \right)}^2}}}\).
Dựa vào đồ thị hàm số ta thấy: Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {0;1} \right)\) nên \(f'\left( x \right) \le 0\,\,\forall x \in \left[ {0;1} \right]\), lại có \( - \dfrac{1}{{{{\left( {x + 2} \right)}^2}}} < 0\,\,\forall x \in \left[ {0;1} \right]\), do đó \(g'\left( x \right) < 0\,\,\forall x \in \left[ {0;1} \right]\), suy ra hàm số \(y = g\left( x \right)\) nghịch biến trên \(\left[ {0;1} \right]\) nên \(\mathop {\min }\limits_{\left[ {0;1} \right]} g\left( x \right) = g\left( 1 \right) = f\left( 1 \right) - \dfrac{2}{3}\).
Vậy \(m \le f\left( 1 \right) - \dfrac{2}{3}\).
Gọi \(m,\,\,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f\left( x \right) = 2x + \cos \dfrac{{\pi x}}{2}\) trên đoạn \(\left[ { - 2;\,\,2} \right].\) Giá trị của \(m + M\) bằng:
Ta có: \(f\left( x \right) = 2x + \cos \dfrac{{\pi x}}{2} \Rightarrow f'\left( x \right) = 2 - \dfrac{\pi }{2}\sin \dfrac{{\pi x}}{2}.\)
Vì \( - 1 \le \sin \dfrac{{\pi x}}{2} \le 1 \Rightarrow - \dfrac{\pi }{2} \le \dfrac{\pi }{2}\sin \dfrac{{\pi x}}{2} \le \dfrac{\pi }{2} \Rightarrow 0 < 2 - \dfrac{\pi }{2} \le 2 - \dfrac{\pi }{2}\sin \dfrac{{\pi x}}{2} \le 2 + \dfrac{\pi }{2}\)
\( \Rightarrow f'\left( x \right) > 0\,\,\forall x \in \left[ { - 2;\,\,2} \right] \Rightarrow \) hàm số \(f\left( x \right) = 2x + \cos \dfrac{{\pi x}}{2}\) là hàm đồng biến trên \(\left[ { - 2;\,\,2} \right].\)
\(\begin{array}{l} \Rightarrow f\left( { - 2} \right) \le f\left( x \right) \le f\left( 2 \right)\,\,\,\forall x \in \left[ { - 2;\,\,2} \right].\\ \Rightarrow \left\{ \begin{array}{l}M = \mathop {\max }\limits_{\left[ { - 2;\,\,2} \right]} f\left( x \right) = f\left( 2 \right) = 3\\m = \mathop {\min }\limits_{\left[ { - 2;\,\,2} \right]} f\left( x \right) = f\left( { - 2} \right) = - 5\end{array} \right.\\ \Rightarrow M + m = 3 + \left( { - 5} \right) = - 2.\end{array}\)
Một mảnh đất hình chữ nhật ABCD có chiều dài \(AB = 25\;{\rm{m}}\), chiều rộng \(AD = 20\;{\rm{m}}\) được chia thành hai phần bằng nhau bởi vạch chắn \(MN\). \(M,N\) lần lượt là trung điểm BC và AD. Một đội xây dựng làm một con đường đi từ A đến C qua vạch chắn MN, biết khi làm đường trên miền ABMN mỗi giờ làm được \(15\;{\rm{m}}\) và khi làm trong miền CDNM mỗi giờ làm được \(30\;{\rm{m}}\). Tính thời gian ngắn nhất mà đội xây dựng làm được con đường đi từ \(A\) đến \(C\).
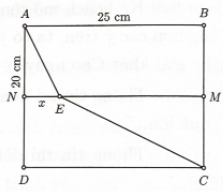
Do cần thời gian xây là ngắn nhất nên con đường làm trên mỗi miền phải là những đường thẳng.
Gọi AE và EC lần lượt là đoạn đường cần làm. Với \(NE = x(\;{\rm{m}})\).
\( \Rightarrow EM = 25 - x(\;{\rm{m}})\).
Ta được \(\left\{ {\begin{array}{*{20}{l}}{AE = \sqrt {A{N^2} + E{N^2}} = \sqrt {100 + {x^2}} }\\{EC = \sqrt {M{C^2} + E{M^2}} = \sqrt {100 + {{(25 - x)}^2}} }\end{array}} \right.\).
\( \Rightarrow \) Thời gian để làm đoạn đường từ \(A\) đến \(C\) là:
\(t(x) = \dfrac{{AE}}{{15}} + \dfrac{{EC}}{{30}} = \dfrac{{\sqrt {100 + {x^2}} }}{{15}} + \dfrac{{\sqrt {{{(25 - x)}^2} + 100} }}{{30}}(\;{\rm{h}}\)
\( \Rightarrow {t^\prime }(x) = \dfrac{x}{{15\sqrt {100 + {x^2}} }} - \dfrac{{25 - x}}{{30\sqrt {{{(25 - x)}^2} + 100} }}.\)
Xét \({t^\prime }(x) = 0 \Leftrightarrow \dfrac{x}{{15\sqrt {100 + {x^2}} }} - \dfrac{{25 - x}}{{30\sqrt {{{(25 - x)}^2} + 100} }} = 0\)
\( \Leftrightarrow 2x\sqrt {{{(25 - x)}^2} + 100} = (25 - x)\sqrt {100 + {x^2}} \)
\( \Leftrightarrow 4{x^2}\left( {{{(25 - x)}^2} + 100} \right) = {(25 - x)^2}\left( {100 + {x^2}} \right)\)
\( \Leftrightarrow 4{x^2}{(25 - x)^2} + 400{x^2} - 100{(25 - x)^2} - {(25 - x)^2}{x^2} = 0\)
\( \Leftrightarrow 4{(25 - x)^2}\left( {{x^2} - 25} \right) + {x^2}\left( {{{20}^2} - {{(25 - x)}^2}} \right) = 0\)
\( \Leftrightarrow (x - 5)\left( {4{{(25 - x)}^2}(x + 5) + {x^2}(45 - x)} \right) = 0 \Leftrightarrow x = 5\)
Ta được \(t(0) = \dfrac{{4 + \sqrt {29} }}{6};t(5) = \dfrac{{2\sqrt 5 }}{3};t(25) = \dfrac{{1 + \sqrt {29} }}{3}\)
Vậy thời gian ngắn nhất mà đội xây dựng làm được con đương đi từ \(A\) đến \(C\) là \(\dfrac{{2\sqrt 5 }}{3}(\;{\rm{h}})\)
Trên đoạn \(\left[ {2;4} \right]\), hàm số \(y = {x^2} + \dfrac{2}{x}\) đạt giá trị lớn nhất tại điểm:
Hàm số đã cho xác định trên \(\left[ {2;4} \right]\).
Ta có: \(y' = 2x - \dfrac{2}{{{x^2}}}\).
\(y' = 0 \Leftrightarrow 2x = \dfrac{2}{{{x^2}}} \Leftrightarrow {x^3} = 1 \Leftrightarrow x = 1 \notin \left[ {2;4} \right]\).
Ta có: \(y\left( 2 \right) = 5,\,\,y\left( 4 \right) = \dfrac{{33}}{2}\).
Vậy \(\mathop {\max }\limits_{\left[ {2;4} \right]} y = y\left( 4 \right) = \dfrac{{33}}{2}\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới đây:
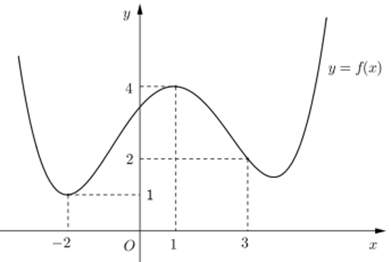
Có bao nhiêu giá trị nguyên của tham số m không vượt quá 2022 để bất phương trình \(\dfrac{m}{{f\left( x \right)}} - \sqrt {mf\left( x \right)} - 1 \ge \dfrac{3}{4}{f^2}\left( x \right)\) đúng với mọi \(x \in \left[ { - 2;3} \right]\)?
Điều kiện: \(mf\left( x \right) \ge 0\).
Dựa vào đồ thị ta thấy: Với \(x \in \left[ { - 2;3} \right]\) thì \(f\left( x \right) \ge 0\) \( \Rightarrow m \ge 0\).
Ta có:
\(\begin{array}{l}\,\,\,\,\,\dfrac{m}{{f\left( x \right)}} - \sqrt {mf\left( x \right)} - 1 \ge \dfrac{3}{4}{f^2}\left( x \right)\\ \Leftrightarrow \dfrac{m}{{f\left( x \right)}} - \sqrt {mf\left( x \right)} + \dfrac{{{f^2}\left( x \right)}}{4} \ge {f^2}\left( x \right) + 1\\ \Leftrightarrow {\left( {\sqrt {\dfrac{m}{{f\left( x \right)}}} - \dfrac{{f\left( x \right)}}{2}} \right)^2} \ge {f^2}\left( x \right) + 1\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt {\dfrac{m}{{f\left( x \right)}}} - \dfrac{{f\left( x \right)}}{2} \ge \sqrt {{f^2}\left( x \right) + 1} \\\sqrt {\dfrac{m}{{f\left( x \right)}}} - \dfrac{{f\left( x \right)}}{2} \le - \sqrt {{f^2}\left( x \right) + 1} \end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}\sqrt m \ge \sqrt {\left[ {{f^2}\left( x \right) + 1} \right]f\left( x \right)} + \dfrac{1}{2}f\left( x \right)\sqrt {f\left( x \right)} \\\sqrt m \le - \sqrt {\left[ {{f^2}\left( x \right) + 1} \right]f\left( x \right)} + \dfrac{1}{2}f\left( x \right)\sqrt {f\left( x \right)} \end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}\sqrt m \ge \mathop {\max }\limits_{\left[ { - 2;3} \right]} \left\{ {\sqrt {\left[ {{f^2}\left( x \right) + 1} \right]f\left( x \right)} + \dfrac{1}{2}f\left( x \right)\sqrt {f\left( x \right)} } \right\}\\\sqrt m \le \mathop {\min }\limits_{\left[ { - 2;3} \right]} \left\{ { - \sqrt {\left[ {{f^2}\left( x \right) + 1} \right]f\left( x \right)} + \dfrac{1}{2}f\left( x \right)\sqrt {f\left( x \right)} } \right\}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt m \ge 4 + 2\sqrt {17} \\\sqrt m \le 4 - 2\sqrt {17} \end{array} \right.\end{array}\)
\( \Rightarrow m \ge {\left( {4 + 2\sqrt {17} } \right)^2} \approx 149,96\).
Kết hợp điều kiện đề bài có $2022-150+1=1873$
\( \Rightarrow \) Có 1873 giá trị m thỏa mãn.
Ông A dự định sử dụng hết 5m2 kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Gọi chiều rộng của bể cá là x (m) \(\left( {x > 0} \right) \Rightarrow \) Chiều dài của bể cá là \(2x\,\,\left( m \right)\)
Gọi h là chiều cao của bể cá ta có \(2{x^2} + 2xh + 4xh = 5 \Leftrightarrow 2{x^2} + 6xh = 5 \Leftrightarrow h = \dfrac{{5 - 2{x^2}}}{{6x}}\)
Khi đó thể tích của bể cá là \(2{x^2}.\dfrac{{5 - 2{x^2}}}{{6x}} = \dfrac{1}{3}\left( {5x - 2{x^3}} \right) = \dfrac{1}{3}f\left( x \right)\)
Xét hàm số \(f\left( x \right) = 5x - 2{x^3}\,\,\left( {x > 0} \right)\) có \(f'\left( x \right) = 5 - 6{x^2} = 0 \Leftrightarrow x = \sqrt {\dfrac{5}{6}} \)
Lập BBT :
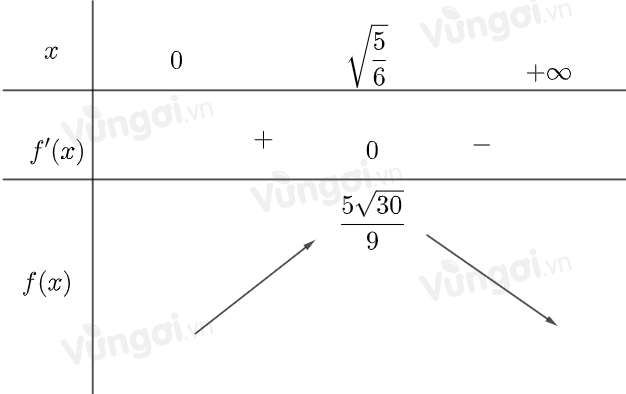
\( \Rightarrow \mathop {\max }\limits_{\left( {0; + \infty } \right)} f\left( x \right) = f\left( {\sqrt {\dfrac{5}{6}} } \right)\)
\( \Rightarrow {V_{\max }} = \dfrac{1}{3}f\left( {\sqrt {\dfrac{5}{6}} } \right) = \dfrac{{5\sqrt {30} }}{{27}} \approx 1,01{m^3}\)
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 1;3} \right]\) và có đồ thị như hình vẽ bên. Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;3} \right]\). Tính \(M - m\).
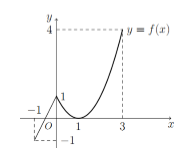
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;3} \right]\) lần lượt là : \(M = 4,\,\,m = - 1 \Rightarrow M - m = 4 - \left( { - 1} \right) = 5\).
Tìm giá trị nhỏ nhất \(m\) của hàm số \(y = {x^3} - 3{x^2}\) trên đoạn \(\left[ { - 1;1} \right].\)
Ta có: \(y' = 3{x^2} - 6x,\,\,\,\,y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left[ { - 1;1} \right]\\x = 2 \notin \left[ { - 1;1} \right]\end{array} \right.\).
Ta có: \(y\left( { - 1} \right) = - 4,\,y\left( 0 \right) = 0,\,y\left( 1 \right) = - 2.\)
Vậy \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = y\left( { - 1} \right) = - 4\).
Đề thi THPT QG 2020 – mã đề 104
Giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^3} - 33x\) trên đoạn \(\left[ {2;19} \right]\) bằng
Xét hàm số: \(f\left( x \right) = {x^3} - 33x\) trên \(\left[ {2;\,\,19} \right]\)
Ta có: \(f'\left( x \right) = 3{x^2} - 33\)
\( \Rightarrow f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 33 = 0\) \( \Leftrightarrow {x^2} = 11 \Leftrightarrow \left[ \begin{array}{l}x = \sqrt {11} \,\, \in \,\,\left[ {2;\,\,19} \right]\\x = - \sqrt {11} \,\, \notin \,\,\left[ {2;\,\,19} \right]\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}f\left( 2 \right) = - 58\\f\left( {\sqrt {11} } \right) = - 22\sqrt {11} \\f\left( {19} \right) = 6232\end{array} \right.\)\( \Rightarrow {f_{\min }} = f\left( {\sqrt {11} } \right) = - 22\sqrt {11} .\)

