Đề thi THPT QG - 2021 - mã 102
Trên đoạn \(\left[ { - 2;1} \right],\) hàm số \(y = {x^3} - 3{x^2} - 1\) đạt giá trị lớn nhất tại điểmTa có: \(y' = 3{x^2} - 6x = 0 \Rightarrow \left[ \begin{array}{l}x = 0\, \in \left[ { - 2;1} \right]\\x = 2\, \notin \left[ { - 2;1} \right]\end{array} \right.\)
\(y\left( { - 2} \right) = - 21;\,\,y\left( 0 \right) = - 1\,\,;\,y\left( 1 \right) = - 3\)
Hàm số đạt giá trị lớn nhất tại điểm \(x = 0\).
Giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} + 2\) trên đoạn \(\left[ { - 1;\,\,1} \right]\) bằng:
Xét hàm số \(y = {x^3} - 3{x^2} + 2\) trên đoạn \(\left[ { - 1;\,\,1} \right]\) ta có:
\(\begin{array}{l}y' = 3{x^2} - 6x \Rightarrow y' = 0\\ \Leftrightarrow 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\, \in \left[ { - 1;\,\,1} \right]\\x = 2\,\, \notin \left[ { - 1;\,\,1} \right]\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}f\left( { - 1} \right) = - 2\\f\left( 0 \right) = 2\\f\left( 1 \right) = 0\end{array} \right. \Rightarrow \mathop {Min}\limits_{\left[ { - 1;\,\,1} \right]} f\left( x \right) = - 2\,\,\,khi\,\,\,x = - 1.\end{array}\)
Gọi S là tập hợp tất cả các giá trị nguyên của tham số thực m sao cho giá trị lớn nhất của hàm số \(y = \left| {\dfrac{1}{4}{x^4} - 14{x^2} + 48x + m - 30} \right|\) trên đoạn \(\left[ {0;2} \right]\) không vượt quá 30. Tổng giá trị của phần tử tập hợp S bằng bao nhiêu ?
Xét hàm số \(f\left( x \right) = \dfrac{1}{4}{x^4} - 14{x^2} + 48x + m - 30\) có \(y' = {x^3} - 28x + 48\).
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 6\\x = 4\\x = 2\end{array} \right.\)
Bảng biến thiên của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {0;2} \right]\):
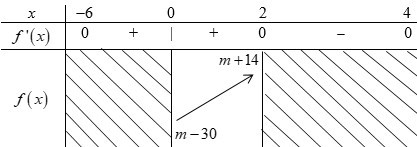
TH1: \(m - 30 \ge 0\) \( \Leftrightarrow m \ge 30\).
\( \Rightarrow \mathop {\max }\limits_{\left[ {0;2} \right]} \left| {f\left( x \right)} \right| = m + 14 \le 30 \Leftrightarrow m \le 16\) (Vô lí).
TH2: \(m - 30 < 0 \le m + 14\) \( \Leftrightarrow - 14 \le m < 30\).
+ Nếu \(m + 14 \ge 30 - m \Leftrightarrow m \ge 8\), kết hợp điều kiện ta có: \(8 \le m < 30\) thì \(\mathop {\max }\limits_{\left[ {0;2} \right]} \left| {f\left( x \right)} \right| = m + 14 \le 30 \Leftrightarrow m \le 16\).
\( \Rightarrow 8 \le m \le 16\).
+ Nếu \(m + 14 < 30 - m \Leftrightarrow m < 8\), kết hợp điều kiện ra có \( - 14 \le m < 8\) thì \(\mathop {\max }\limits_{\left[ {0;2} \right]} \left| {f\left( x \right)} \right| = 30 - m \le 30 \Leftrightarrow m \ge 0\).
\( \Rightarrow 0 \le m < 8\)
Vậy trường hợp 2 ta có \(0 \le m \le 16\) thỏa mãn.
TH3: \(m + 14 < 0 \Leftrightarrow m < - 14\).
\( \Rightarrow \mathop {\max }\limits_{\left[ {0;2} \right]} \left| {f\left( x \right)} \right| = 30 - m \le 30 \Leftrightarrow m \ge 0\) (vô lí).
Từ các trường hợp \( \Rightarrow m \in \left[ {0;16} \right]\).
\( \Rightarrow S = \left\{ {0;1;2;3;...;16} \right\}\).
Vậy tổng các phần tử của \(S\) bằng \(0 + 1 + 2 + ... + 16 = \dfrac{{16.17}}{2} = 136\).
Tìm giá trị nhỏ nhất của hàm số \(y = x + \dfrac{{16}}{{\sqrt x }}.\)
Xét hàm số \(y = x + \dfrac{{16}}{{\sqrt x }}\) ta có:
TXĐ: \(D = \left( {0; + \infty } \right).\)
\(\begin{array}{l}y' = 1 - \dfrac{{16.\dfrac{1}{{2\sqrt x }}}}{{\sqrt x }} = 1 - \dfrac{8}{{x\sqrt x }} = \dfrac{{x\sqrt x - 8}}{{x\sqrt x }}\\ \Rightarrow y' = 0 \Leftrightarrow x\sqrt x - 8 = 0 \Leftrightarrow x\sqrt x = 8\\ \Leftrightarrow {\left( {\sqrt x } \right)^3} = {2^3} \Leftrightarrow \sqrt x = 2 \Leftrightarrow x = 4\,\,\left( {tm} \right)\end{array}\)
Ta có bảng xét dấu:
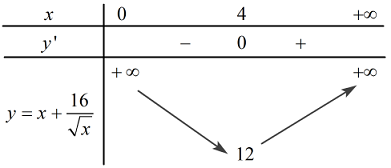
\( \Rightarrow \mathop {Min}\limits_{\left( {0; + \infty } \right)} y = 12\) khi \(x = 4.\)
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) sao cho giá trị nhỏ nhất của hàm số \(y = \left| {{x^2} - 2x + m} \right|\) trên đoạn \(\left[ {0;3} \right]\) bằng 5. Tổng tất cả các phần tử của \(S\) bằng:
Xét hàm số \(f\left( x \right) = {x^2} - 2x + m\) trên đoạn \(\left[ {0;3} \right]\) ta có:
\(\begin{array}{l}f'\left( x \right) = 2x - 2\\f'\left( x \right) = 0 \Leftrightarrow 2x - 2 = 0 \Leftrightarrow x = 1\end{array}\)
Ta có \(f\left( 0 \right) = m,\,\,f\left( 1 \right) = m - 1,\,\,f\left( 3 \right) = m + 3\).
Dễ thấy $m - 1 < m < m + 3$ nên ta có BBT của hàm số \(f\left( x \right)\) trên \(\left[ {0;3} \right]\) như sau:
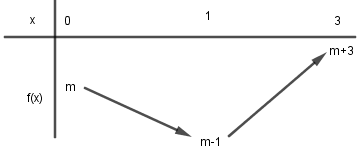
+) TH1: \(m - 1 \ge 0 \Leftrightarrow m \ge 1\) thì:
\(\mathop {\min }\limits_{\left[ {0;3} \right]} \left| {f\left( x \right)} \right| = m - 1 = 5\) \( \Leftrightarrow m = 6\left( {TM} \right)\)
+) TH2: \(m - 1 < 0 \le m + 3 \Leftrightarrow - 3 \le m < 1\) thì:
\(\mathop {\min }\limits_{\left[ {0;3} \right]} \left| {f\left( x \right)} \right| = 0 \ne 5\) (mẫu thuẫn giải thiết) nên loại.
+) TH3: \(m + 3 < 0 \Leftrightarrow m < - 3\) thì:
\(\mathop {\min }\limits_{\left[ {0;3} \right]} \left| {f\left( x \right)} \right| = - m - 3 = 5\)\( \Leftrightarrow m = - 8\left( {TM} \right)\)
Vậy \(m \in \left\{ {6; - 8} \right\}\) nên tổng các giá trị của \(m\) là \(6 + \left( { - 8} \right) = - 2\).
Tìm giá trị lớn nhất của hàm số \(y = f\left( x \right) = \sqrt {x - 1} + \sqrt {5 - x} \) trên đoạn \(\left[ {1;5} \right]\).
TXĐ: \(\left\{ \begin{array}{l}x - 1 \ge 0\\5 - x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x \le 5\end{array} \right. \Rightarrow D = \left[ {1;5} \right]\).
Ta có \(f'\left( x \right) = \dfrac{1}{{2\sqrt {x - 1} }} - \dfrac{1}{{2\sqrt {5 - x} }} = \dfrac{{\sqrt {5 - x} - \sqrt {x - 1} }}{{2\sqrt {x - 1} .\sqrt {5 - x} }}\).
Cho \(f'\left( x \right) = 0 \Leftrightarrow \sqrt {5 - x} = \sqrt {x - 1} \) \( \Leftrightarrow 5 - x = x - 1\) \( \Leftrightarrow 2x = 6\) \( \Leftrightarrow x = 3 \in \left[ {1;5} \right]\).
Mặt khác \(f\left( 1 \right) = 2,\,\,f\left( 3 \right) = 2\sqrt 2 ,\,\,f\left( 5 \right) = 2\).
Vậy \(\mathop {max}\limits_{\left[ {1;5} \right]} f\left( x \right) = f\left( 3 \right) = 2\sqrt 2 \).
Gọi \(S\) là tập hợp tất cả các giá trị nguyên dương của tham số \(m\) để bất phương trình \({x^6} + 6{x^4} - {m^3}{x^3} + 13{x^2} - mx + 10 \ge 0\) nghiệm đúng với mọi \(x \in [1;4]\). Tích tất cả các phần tử của \(S\) là
Bước 1: Đưa về dạng \(f\left( x \right) \ge f\left( {mx} \right)\) với \(f(t) = {t^3} + t\)
Ta có:
\({x^6} + 6{x^4} - {m^3}{x^3} + 13{x^2} - mx + 10 \ge 0\)
\( \Leftrightarrow {x^6} + 6{x^4} + 13{x^2} + 10\)\( \ge {m^3}{x^3} + mx\)
\( \Leftrightarrow \left( {{x^6} + 6{x^4} + 12{x^2} + 8} \right)\)\( + \left( {{x^2} + 2} \right) \ge {m^3}{x^3} + mx\)
\( \Leftrightarrow {\left( {{x^2} + 2} \right)^3} + \left( {{x^2} + 2} \right)\)\( \ge {(mx)^3} + (mx)(*)\)
Bước 2: Khảo sát hàm \(f(t) = {t^3} + t\) và giải \(f\left( x \right) \ge f\left( {mx} \right)\)
Ta có hàm số \(f(t) = {t^3} + t\)
\( \Rightarrow {f^\prime }(t) = 3{t^2} + 1 > 0\)
\( \Rightarrow f(t)\) luôn đồng biến.
Khi đó:
\((*) \Leftrightarrow f\left( {{x^2} + 2} \right) \ge f(mx)\)\( \Leftrightarrow {x^2} + 2 \ge mx\)
Bước 3: Giải \({x^2} + 2 \ge mx\forall x \in [1;4]\), kết hợp với điều kiện m nguyên dương để tìm số tích các phần tử của S.
Do đó, \({x^6} + 6{x^4} - {m^3}{x^3} + 13{x^2} - mx\)\( + 10 \ge 0\)\(\forall x \in [1;4]\)
\( \Leftrightarrow {x^2} + 2 \ge mx\forall x \in [1;4]\)\( \Leftrightarrow x + \dfrac{2}{x} \ge m\forall x \in [1;4](**)\)
\( \Rightarrow 2\sqrt 2 \ge m\) (Do áp dụng BĐT Cauchy, \(\forall x \in [1;4],x + \dfrac{2}{x} \ge 2\sqrt 2 \) )
Mà \(m\) là số nguyên dương nên \(m \in \{ 1;2\} \Rightarrow S = \{ 1;2\} \).
Vậy tích các phần tử của S là 2.
Cho hàm số $f\left( x \right)$ xác định trên $\left[ {0;2} \right]$ và có GTNN trên đoạn đó bằng $5$. Chọn kết luận đúng:
GTNN của $f\left( x \right)$ trên $\left[ {0;2} \right]$ bằng $5$ nên $f\left( x \right) \geqslant 5,\forall x \in \left[ {0;2} \right] \Rightarrow f\left( 2 \right) \geqslant 5$.
Giá trị nhỏ nhất của hàm số $y = 2x + \cos x$ trên đoạn $\left[ {0;1} \right]$ là :
Ta có $y' = 2 - \sin x > 0{\mkern 1mu} {\mkern 1mu} \forall x \in R \Rightarrow $ Hàm số luôn đồng biến trên $\left[ {0;1} \right]$
$ \Rightarrow \mathop {\min }\limits_{\left[ {0;1} \right]} y = y\left( 0 \right) = 1$.
Cho hàm số $f\left( x \right)$ xác định và liên tục trên $R$, có $\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty $ , khi đó:
Hàm số $y = f\left( x \right)$ có $\mathop {\lim }\limits_{x \to + \infty }f(x) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty $ thì không có GTLN, GTNN trên $R$ vì không tồn tại số $M,m$ để $f\left( x \right) \leqslant M,f\left( x \right) \geqslant m,\forall x \in R$.
Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
${\rm{\;}}x > 1 \Leftrightarrow x - 1 > 0$
$ \Rightarrow y = x - 1 + \dfrac{4}{{x - 1}} \ge 2\sqrt {\left( {x - 1} \right).\dfrac{4}{{x - 1}}} = 2.2 = 4$
Dấu bằng xảy ra $ \Leftrightarrow x - 1 = \dfrac{4}{{x - 1}} \Leftrightarrow {\left( {x - 1} \right)^2} = 4 \Leftrightarrow x = 3$.
Vậy GTNN của hàm số là $m=4$ khi $x=3$.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ, chọn kết luận đúng:
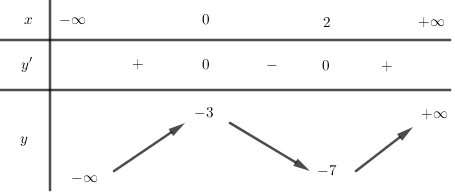
Ta có:
+) $\mathop {\max }\limits_{\left[ { - 3;0} \right]} f\left( x \right) = f\left( 0 \right) = - 3$ nên A sai.
+) $\mathop {\min }\limits_{\left[ {1;3} \right]} f\left( x \right) = f\left( 2 \right) = - 7$ nên B đúng.
+) Vì $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty $ nên không tồn tại $\mathop {\min}\limits_{\left( { - \infty ;2} \right]} f\left( x \right)$ nên C sai.
+) $\mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 0 \right) = - 3$ nên D sai.
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
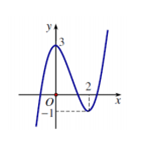
A sai vì $y=3$ là giá trị cực đại của hàm số, không phải giá trị lớn nhất.
B sai vì hàm số đồng biến trên các khoảng $\left( { - \infty ;0} \right),\left( {2; + \infty } \right)$.
C sai vì $x=2$ là điểm cực tiểu của hàm số không phải giá trị cực tiểu.
D đúng vì trên đoạn $\left[ {0;4} \right]$ thì hàm số đạt GTNN (cũng là giá trị cực tiểu) bằng $ - 1$ đạt được tại $x = 2$.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
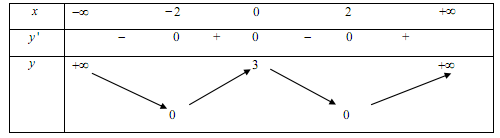
Khẳng định nào sau đây là khẳng định đúng?
Đáp án A: Hàm số đạt cực đại tại $x = 0$ và $y = 3$ là giá trị cực đại của hàm số nên A sai.
Đáp án B: GTNN và giá trị cực tiểu của hàm số là $y = 0$ nên B đúng và C sai.
Đáp án D: Hàm số không có GTLN vì $\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty $.
Tìm giá trị lớn nhất của hàm số $y = {x^3} - 5{{\text{x}}^2} + 3{\text{x}} - 1$ trên đoạn $\left[ {2;4} \right]$
$y' = 3{x^2} - 10x + 3 = 0 \Leftrightarrow \left[ \begin{gathered}x = 3 \in \left[ {2;4} \right] \hfill \\x = \dfrac{1}{3} \notin \left[ {2;4} \right] \hfill \\ \end{gathered} \right.$
$f\left( 2 \right) = - 7,f\left( 3 \right) = - 10,f\left( 4 \right) = - 5$
Vậy giá trị lớn nhất của hàm số $y = {x^3} - 5{{\text{x}}^2} + 3{\text{x}} - 1$ trên đoạn $\left[ {2;4} \right]$ là $M = - 5$
Tìm GTLN và GTNN của hàm số $y = {x^5} - 5{x^4} + 5{x^3} + 1$ trên đoạn $\left[ { - 1;2} \right]$
Ta có: $y' = 5{{\text{x}}^4} - 20{{\text{x}}^3} + 15{{\text{x}}^2} = 0 \Leftrightarrow 5{x^2}\left( {{x^2} - 4x + 3} \right) = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \in \left[ { - 1;2} \right] \hfill \\x = 1 \in \left[ { - 1;2} \right] \hfill \\x = 3 \notin \left[ { - 1;2} \right] \hfill \\ \end{gathered} \right.$
$f( - 1) = - 10, f(0) = 1,$ $ f(1) = 2, f(2) = - 7$
Vậy giá trị lớn nhất, nhỏ nhất của hàm trên $\left[ { - 1;2} \right]$ lần lượt là $2$ và $ - 10$
Giá trị lớn nhất của hàm số $f\left( {\text{x}} \right) = \dfrac{{6 - 8{\text{x}}}}{{{x^2} + 1}}$ trên tập xác định của nó là:
TXĐ: $D=R$
Ta có: $f'\left( x \right) = \dfrac{{8{{\text{x}}^2} - 12{\text{x}} - 8}}{{{{\left( {{x^2} + 1} \right)}^2}}}$
$f'\left( x \right) = 0 \Leftrightarrow x = 2$ hoặc $x = - \dfrac{1}{2}$
$\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = 0$
Bảng biến thiên
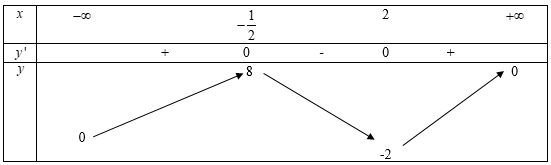
Vậy giá trị lớn nhất của hàm số là $y = 8$ tại $x = - \dfrac{1}{2}$
Gọi giá trị lớn nhất và nhỏ nhất của hàm số $y = {x^4} + 2{x^2} - 1$ trên đoạn $\left[ { - 1;2} \right]$ lần lượt là $M$ và $m$. Khi đó giá trị của $M.m$ là:
TXĐ: $D=R$
Ta có: $y' = 4{{\text{x}}^3} + 4{\text{x}}$$ \Rightarrow y' = 0 \Leftrightarrow x = 0 \in \left[ { - 1;2} \right]$
$f( - 1) = 2,{\text{ f(0) = }} - 1,{\text{ f(2) = 23}}$
Ta thấy GTLN và GTNN lần lượt là $M = 23,m = - 1 \Rightarrow M.m = 23.\left( { - 1} \right) = - 23$
Cho hàm số $y = x + \dfrac{1}{x}.$ Giá trị nhỏ nhất của hàm số trên khoảng $\left( {0;\, + \infty } \right)$ là:
TXĐ: \(R\backslash \left\{ 0 \right\}\)
$y' = 1 - \dfrac{1}{{{x^2}}} = \dfrac{{{x^2} - 1}}{{{x^2}}}$
$y' = 0 \Leftrightarrow \dfrac{{{x^2} - 1}}{{{x^2}}} = 0 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow x=1 (tm) $ hoặc $x=-1 (ktm)$
Bảng biến thiên:
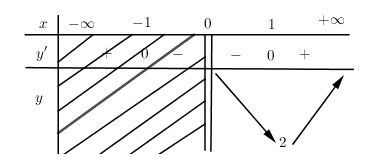
$ \Rightarrow \mathop {Min}\limits_{x \in \left( {0; + \infty } \right)} \,y = f\left( 1 \right) = 2$
Cho hàm số $y = \dfrac{{2mx + 1}}{{m - x}}.$ Giá trị lớn nhất của hàm số trên $\left[ {2;3} \right]$ bằng $\dfrac{{ - 1}}{3}$ khi m bằng:
\(D = \mathbb{R}\backslash \left\{ m \right\}{\rm{ }} \Rightarrow {\rm{m}} \notin \left[ {2;3} \right]\)
\(\begin{array}{l}y = \dfrac{{2mx + 1}}{{ - x + m}}\\ \Rightarrow y' = \dfrac{{2m\left( { - x + m} \right) + 1.\left( {2mx + 1} \right)}}{{{{\left( { - x + m} \right)}^2}}} = \dfrac{{2{m^2} + 1}}{{{{\left( { - x + m} \right)}^2}}} > 0\,,\forall x \in \left[ {2;3} \right]\end{array}\)
Hàm số luôn đồng biến trên \(\left[ {2;3} \right]\)
\(\begin{array}{l} \Rightarrow Max\,y = f\left( 3 \right) = \dfrac{{6m + 1}}{{m - 3}}\\Max\,y = \dfrac{{ - 1}}{3} \Leftrightarrow \dfrac{{6m + 1}}{{m - 3}} = \dfrac{{ - 1}}{3} \Leftrightarrow 18m + 3 = - m + 3 \Leftrightarrow 19m = 0 \Leftrightarrow m = 0(TMDK)\end{array}\)

