Câu hỏi:
2 năm trước
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) sao cho giá trị nhỏ nhất của hàm số \(y = \left| {{x^2} - 2x + m} \right|\) trên đoạn \(\left[ {0;3} \right]\) bằng 5. Tổng tất cả các phần tử của \(S\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: a
Xét hàm số \(f\left( x \right) = {x^2} - 2x + m\) trên đoạn \(\left[ {0;3} \right]\) ta có:
\(\begin{array}{l}f'\left( x \right) = 2x - 2\\f'\left( x \right) = 0 \Leftrightarrow 2x - 2 = 0 \Leftrightarrow x = 1\end{array}\)
Ta có \(f\left( 0 \right) = m,\,\,f\left( 1 \right) = m - 1,\,\,f\left( 3 \right) = m + 3\).
Dễ thấy $m - 1 < m < m + 3$ nên ta có BBT của hàm số \(f\left( x \right)\) trên \(\left[ {0;3} \right]\) như sau:
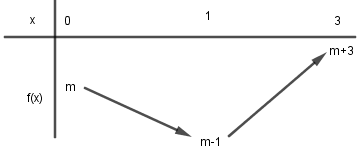
+) TH1: \(m - 1 \ge 0 \Leftrightarrow m \ge 1\) thì:
\(\mathop {\min }\limits_{\left[ {0;3} \right]} \left| {f\left( x \right)} \right| = m - 1 = 5\) \( \Leftrightarrow m = 6\left( {TM} \right)\)
+) TH2: \(m - 1 < 0 \le m + 3 \Leftrightarrow - 3 \le m < 1\) thì:
\(\mathop {\min }\limits_{\left[ {0;3} \right]} \left| {f\left( x \right)} \right| = 0 \ne 5\) (mẫu thuẫn giải thiết) nên loại.
+) TH3: \(m + 3 < 0 \Leftrightarrow m < - 3\) thì:
\(\mathop {\min }\limits_{\left[ {0;3} \right]} \left| {f\left( x \right)} \right| = - m - 3 = 5\)\( \Leftrightarrow m = - 8\left( {TM} \right)\)
Vậy \(m \in \left\{ {6; - 8} \right\}\) nên tổng các giá trị của \(m\) là \(6 + \left( { - 8} \right) = - 2\).
Hướng dẫn giải:
- Xét hàm số \(f\left( x \right) = {x^2} - 2x + m\) trên đoạn \(\left[ {0;3} \right]\), tìm GTLN, GTNN của hàm số trên \(\left[ {0;3} \right]\).
- Từ đó suy ra GTLN, GTNN của hàm số \(y = \left| {f\left( x \right)} \right|\).
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
