Trả lời bởi giáo viên
Đáp án đúng: d
Xét hàm số \(y = x + \dfrac{{16}}{{\sqrt x }}\) ta có:
TXĐ: \(D = \left( {0; + \infty } \right).\)
\(\begin{array}{l}y' = 1 - \dfrac{{16.\dfrac{1}{{2\sqrt x }}}}{{\sqrt x }} = 1 - \dfrac{8}{{x\sqrt x }} = \dfrac{{x\sqrt x - 8}}{{x\sqrt x }}\\ \Rightarrow y' = 0 \Leftrightarrow x\sqrt x - 8 = 0 \Leftrightarrow x\sqrt x = 8\\ \Leftrightarrow {\left( {\sqrt x } \right)^3} = {2^3} \Leftrightarrow \sqrt x = 2 \Leftrightarrow x = 4\,\,\left( {tm} \right)\end{array}\)
Ta có bảng xét dấu:
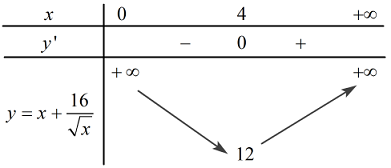
\( \Rightarrow \mathop {Min}\limits_{\left( {0; + \infty } \right)} y = 12\) khi \(x = 4.\)
Hướng dẫn giải:
Cách 1:
+) Tìm GTLN và GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {a;\;b} \right]\) bằng cách:
+) Giải phương trình \(y' = 0\) tìm các nghiệm \({x_i}.\)
+) Tính các giá trị \(f\left( a \right),\;f\left( b \right),\;\;f\left( {{x_i}} \right)\;\;\left( {{x_i} \in \left[ {a;\;b} \right]} \right).\) Khi đó:
\(\mathop {\min }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \min \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\},\;\;\mathop {\max }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \max \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\}.\)
Cách 2: Sử dụng chức năng MODE 7 để tìm GTLN, GTNN của hàm số trên \(\left[ {a;\;b} \right].\)
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
