Cho hàm số $y = {x^3} - 3m{x^2} + 6$, giá trị nhỏ nhất của hàm số trên $\left[ {0;3} \right]$ bằng $2$ khi:
TXĐ: $D = \mathbb{R}$
$y' = 3{x^2} - 6mx.$
Ta có: $y' = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \Rightarrow y = 6 \hfill \\x = 2m \Rightarrow y = - 4{m^3} + 6 \hfill \\ \end{gathered} \right.$
$y^{\prime}=0 \Leftrightarrow\left[\begin{array}{c}x=0 \Rightarrow y=6 \\ x=2 m \Rightarrow y=-4 m^{3}+6\end{array}\right.$
Xét TH1: $m = 0$. Hàm số đồng biến trên $\left[ {0;3} \right]$ $ \Rightarrow \mathop {Min}\limits_{\left[ {0;3} \right]} y = y\left( 0 \right) = 6 \Rightarrow $ loại.
Xét TH2: $m \geqslant \dfrac{3}{2} \Rightarrow 2m \ge 3 > 0$. Khi đó, hàm số nghịch biến trên $\left[ {0;3} \right] \subset \left[ {0;2m} \right]$
$ \Rightarrow \mathop {Min}\limits_{\left[ {0;3} \right]} y = y\left( 3 \right) = 33 - 27m = 2 \Rightarrow m = \dfrac{{31}}{{27}} < \dfrac{3}{2}$(loại)
Xét TH3: $\dfrac{3}{2} > m > 0 \Rightarrow 3 > 2m > 0$ thì đồ thị hàm số có điểm cực đại là $\left( {0;6} \right)$ và điểm cực tiểu là $\left( {2m, - 4{m^3} + 6} \right).$
Khi đó , GTNN trên $\left[ {0;3} \right]$ là $y\left( {2m} \right) = - 4{m^3} + 6$ $ \Rightarrow - 4{m^3} + 6 = 2 \Leftrightarrow {m^3} = 1 \Leftrightarrow m = 1$ (thỏa mãn)
Xét TH4: $m < 0 \Rightarrow \left( {0;6} \right)$ là điểm cực tiểu của đồ thị hàm số và trên $\left[ {0;3} \right]$ hàm số đồng biến.
$ \Rightarrow {y_{min}} = 6 \Rightarrow $ loại.
Vậy $m = 1$ là giá trị cần tìm.
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;2} \right]\).
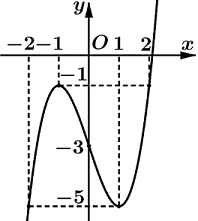
Dựa vào đồ thị hàm số ta có: \(\left\{ \begin{array}{l}m = \mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 5\\M = \mathop {{\rm{max}}}\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 1\end{array} \right.\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình dưới. Gọi \(a,\,\,A\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của \(f\left( {x + 1} \right)\) trên đoạn \(\left[ { - 1;\,\,0} \right].\) Giá trị \(a + A\) bằng:
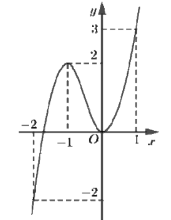
Đặt \(x + 1 = t.\) Khi đó: \(x \in \left[ { - 1;\,\,0} \right] \Rightarrow t \in \left[ {0;\,\,1} \right].\)
Dựa vào đồ thị hàm số ta thấy: \(\left\{ \begin{array}{l}a = \mathop {Min}\limits_{\left[ {0;\,1} \right]} f\left( t \right) = 0\,\,\,khi\,\,\,t = 0 \Rightarrow x = - 1.\\A = \mathop {Max}\limits_{\left[ {0;\,1} \right]} f\left( t \right) = 3\,\,\,\,khi\,\,\,t = 1 \Rightarrow x = 0.\end{array} \right.\)
\( \Rightarrow a + A = 0 + 3 = 3.\)
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;4} \right]\) và có đồ thị như hình vẽ
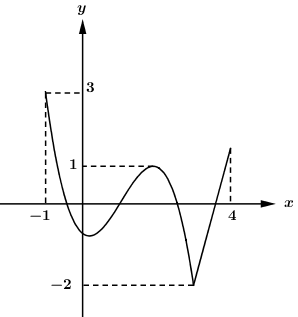
Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn \(\left[ { - 10;10} \right]\) để bất phương trình \(\left| {f\left( x \right) + m} \right| < 2m\) đúng với mọi x thuộc đoạn \(\left[ { - 1;4} \right]\)?
Ta có: \(\left| {f\left( x \right) + m} \right| < 2m\)
\(\Leftrightarrow - 2m < f\left( x \right) + m < 2m\)
\(\Leftrightarrow - 3m < f\left( x \right) < m\)
\( \Leftrightarrow \left\{ \begin{array}{l} - 3m < \mathop {\min }\limits_{\left[ { - 1;4} \right]} f\left( x \right)\\\mathop {\max }\limits_{\left[ { - 1;4} \right]} f\left( x \right) < m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3m < - 2\\3 < m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{2}{3}\\m > 3\end{array} \right. \Leftrightarrow m > 3\).
Kết hợp điều kiện đề bài \( \Rightarrow m \in \left( {3;10} \right],\,\,m \in \mathbb{Z} \Rightarrow m \in \left\{ {4;5;6;7;8;9;10} \right\}\).
Vậy có 7 giá trị của m thỏa mãn yêu cầu bài toán.
Gọi \(M,\,\,N\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right) = \left| {x - 3} \right|\sqrt {x + 1} \) trên đoạn \(\left[ {0;4} \right]\). Tính\(M + 2N\).
Hàm số xác định trên \(\left[ {0;4} \right]\).
Ta có: \(f\left( x \right) = \left| {x - 3} \right|\sqrt {x + 1} = \sqrt {\left( {x + 1} \right){{\left( {x - 3} \right)}^2}} \).
Xét hàm số \(g\left( x \right) = \left( {x + 1} \right){\left( {x - 3} \right)^2}\) trên đoạn \(\left[ {0;4} \right]\) ta có:
\(\begin{array}{l}g'\left( x \right) = {\left( {x - 3} \right)^2} + \left( {x + 1} \right).2\left( {x - 3} \right)\\g'\left( x \right) = \left( {x - 3} \right)\left( {x - 3 + 2x + 2} \right)\\g'\left( x \right) = \left( {x - 3} \right)\left( {3x - 1} \right)\\g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3 \in \left[ {0;4} \right]\\x = \dfrac{1}{3} \in \left[ {0;4} \right]\end{array} \right.\end{array}\)
Ta có: \(g\left( 0 \right) = 9,\,\,g\left( {\dfrac{1}{3}} \right) = \dfrac{{256}}{{27}},\,\,g\left( 3 \right) = 0,\,\,g\left( 4 \right) = 5\).
Vậy \(\left\{ \begin{array}{l}M = \mathop {\max }\limits_{\left[ {0;4} \right]} f\left( x \right) = \sqrt {g\left( {\dfrac{1}{3}} \right)} = \dfrac{{16\sqrt 3 }}{9}\\N = \mathop {\min }\limits_{\left[ {0;4} \right]} f\left( x \right) = \sqrt {g\left( 0 \right)} = 0\end{array} \right.\)\( \Rightarrow M + 2N = \dfrac{{16\sqrt 3 }}{9}\).
Một sợi dây kim loại dài \(a\,\,\left( {{\rm{cm}}} \right)\) . Người ta cắt sợi dây đó thành hai đoạn, trong đó một đoạn có độ dài \(x\,\,\left( {{\rm{cm}}} \right)\) được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông \(\left( {a > x > 0} \right).\) Tìm \(x\) để hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.
Do \(x\) là độ dài của đoạn dây cuộn thành hình tròn \(\left( {0 < x < a} \right)\). Suy ra chiều dài đoạn còn lại là \(a - x\).
Gọi \(r\) là bán kính của đường tròn. Chu vi đường tròn: \(2\pi r = x\)\( \Rightarrow r = \dfrac{x}{{2\pi }}\).
Do đó diện tích hình tròn là: \({S_1} = \pi .{r^2}\)\( = \dfrac{{{x^{\rm{2}}}}}{{4\pi }}\).
Chu vi hình vuông là \(a - x \Rightarrow \) Cạnh hình vuông là \(\dfrac{{a - x}}{4}\). Do đó diện tích hình vuông: \({S_2} = {\left( {\dfrac{{a - x}}{4}} \right)^2}\).
Tổng diện tích hai hình:
\(\begin{array}{l}S = \dfrac{{{x^2}}}{{4\pi }} + {\left( {\dfrac{{a - x}}{4}} \right)^2}\\\,\,\,\, = \dfrac{{4{x^2} + \pi {{\left( {a - x} \right)}^2}}}{{16\pi }}\\\,\,\,\,\, = \dfrac{{\left( {4 + \pi } \right).{x^2} - 2a\pi x + \pi {a^2}}}{{16\pi }}\end{array}\)
Xét hàm số \(S\left( x \right) = \dfrac{{\left( {4 + \pi } \right).{x^2} - 2a\pi x + \pi {a^2}}}{{16\pi }}\) ta có:\(S'\left( x \right) = \dfrac{{2\left( {4 + \pi } \right).x - 2a\pi }}{{16\pi }} = \dfrac{{\left( {4 + \pi } \right).x - a\pi }}{{8\pi }}\).
Cho\(S'\left( x \right) = 0 \Leftrightarrow \left( {4 + \pi } \right)x - a\pi = 0 \Leftrightarrow x = \dfrac{{a\pi }}{{4 + \pi }}\). Ta có BBT như sau :
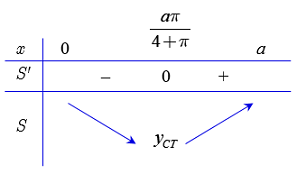
Suy ra hàm \(S\) chỉ có một cực trị và là cực tiểu tại \(x = \dfrac{{a\pi }}{{4 + \pi }}\).
Do đó \(S\) đạt giá trị nhỏ nhất tại \(x = \dfrac{{a\pi }}{{4 + \pi }}\).
Gọi \(M\) và \(m\) là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 2{\sin ^2}x - \cos x + 1\). Khi đó, giá trị của tổng \(M + m\) bằng:
\(\begin{array}{l}\,\,\,\,\,\,\,y = 2{\sin ^2}x - \cos x + 1\\ \Rightarrow y = 2\left( {1 - {{\cos }^2}x} \right) - \cos x + 1\\ \Rightarrow y = - 2{\cos ^2}x - \cos x + 3\end{array}\)
Đặt \(\cos x = t\,\,\,\,\left( { - 1 \le t \le 1} \right)\), hàm số trở thành: \(y = - 2{t^2} - t + 3.\)
Ta có: \(y' = - 4t - 1 = 0 \Rightarrow t = - \dfrac{1}{4}\,\,\,\left( {tm} \right)\).
Bảng biến thiên:
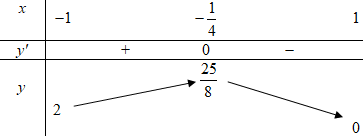
Từ BBT ta suy ra \(M = \dfrac{{25}}{8},\,\,m = 0\).
Vậy \(M + m = \dfrac{{25}}{8}\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ. Đặt \(g\left( x \right) = 2f\left( x \right) - {x^2}\). Khi đó giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { - 2;4} \right]\) là:
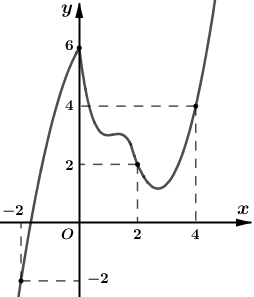
Ta có \(g\left( x \right) = 2f\left( x \right) - {x^2}\) \( \Rightarrow g'\left( x \right) = 2f'\left( x \right) - 2x\)
Cho \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = x\,\,\,\left( 1 \right)\).
Nghiệm của phương trình (1) là hoành độ giao điểm của hai đồ thị hàm số \(y = f'\left( x \right);\,\,y = x.\)
Vẽ đường thẳng \(y = x\) và đồ thị hàm số \(y = f'\left( x \right)\) trên cùng hệ trục tọa độ:
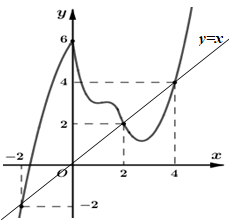
Dựa vào đồ thị ta thấy đồ thị hai hàm số \(y = f'\left( x \right);\,\,y = x\) cắt nhau tại 3 điểm có hoành độ là \( - 2;2;4.\)
\( \Rightarrow g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 2\\x = 4\end{array} \right.\)
Bảng biến thiên đồ thị hàm số \(y = g\left( x \right)\):
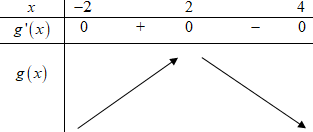
Dựa vào bảng biến thiên ta thấy giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { - 2;4} \right]\) là \(g\left( 2 \right)\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Xét hàm số \(g\left( x \right) = f\left( {{x^3} + 2x} \right) + m\). Giá trị của tham số \(m\) để giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ {0;1} \right]\) bằng \(9\) là:
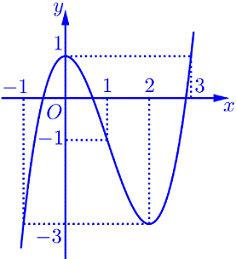
Ta có : \(g'\left( x \right) = \left( {3{x^2} + 2} \right).f'\left( {{x^3} + 2x} \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}3{x^2} + 2 = 0\\f'\left( {{x^3} + 2x} \right) = 0\end{array} \right. \Leftrightarrow f'\left( {{x^3} + 2x} \right) = 0\) (Do phương trình \(3{x^2} + 2 = 0\) vô nghiệm).
Từ đồ thị hàm số \(f\left( x \right)\) đã cho ta có : \(f'\left( {{x^3} + 2x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^3} + 2x = 0\\{x^3} + 2x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = {x_0} \approx 0,77\end{array} \right.\)
Hàm số \(g\left( x \right)\) trên đoạn \(\left[ {0;1} \right]\) có :
\(\begin{array}{l}g\left( 0 \right) = f\left( 0 \right) + m = m + 1\\g\left( {{x_0}} \right) = f\left( 2 \right) + m = m - 3\\g\left( 1 \right) = f\left( 3 \right) + m = m + 1\end{array}\)
Do đó, \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = g\left( 0 \right) = g\left( 1 \right) = m + 1\).
Theo giả thiết, giá trị lớn nhất của hàm số \(g\left( x \right)\) trên \(\left[ {0;1} \right]\) bằng 9 nên \(m + 1 = 9 \Leftrightarrow m = 8\).
Vậy \(m = 8.\)
Hàm số nào dưới đây có giá trị nhỏ nhất trên tập xác định?
Các hàm số đã cho đều có TXĐ:\(D = \mathbb{R}\)
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} - 3x + 2} \right) = - \infty \\\mathop {\lim }\limits_{x \to + \infty } \left( { - 2{x^3} + 3{x^2} - 1} \right) = - \infty \\\mathop {\lim }\limits_{x \to \pm \infty } \left( {{x^4} - 2{x^2} - 1} \right) = + \infty \\\mathop {\lim }\limits_{x \to \pm \infty } \left( { - {x^4} + 4{x^2}} \right) = - \infty \end{array}\)
Do đó, hàm số có giá trị nhỏ nhất trên tập xác định là \(y = {x^4} - 2{x^2} - 1\).
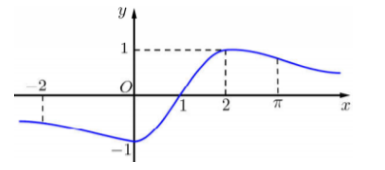
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Gọi \(M\) và \(m\) tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( {1 - 2\cos x} \right)\) trên \(\left[ {0;\,\,\dfrac{{3\pi }}{2}} \right]\). Giá trị của \(M + m\) bằng
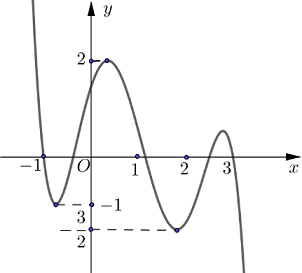
Đặt \(t = 1 - 2\cos x\). Với \(x \in \left[ {0;\,\,\dfrac{{3\pi }}{2}} \right]\) thì \(\cos x \in \left[ { - 1;1} \right] \Rightarrow \)\(1 - 2\cos x \in \left[ { - 1;3} \right] \Rightarrow t \in \left[ { - 1;3} \right].\)
Khi đó ta có \(y = f\left( t \right)\) với \(t \in \left[ { - 1;3} \right]\).
Quan sát đồ thị hàm số \(y = f\left( t \right)\) trên đoạn \(\left[ { - 1;3} \right]\), ta thấy GTLN của hàm số là 2, GTNN của hàm số là \( - \dfrac{3}{2}\)
\( \Rightarrow M = 2,\,\,m = - \dfrac{3}{2} \Rightarrow M + m = \dfrac{1}{2}\)
Cho các số thực $x, y$ thỏa mãn ${\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} + 2xy \leqslant 32.$ Giá trị nhỏ nhất $m$ của biểu thức $A = {x^3} + {y^3} + 3\left( {xy - 1} \right)\left( {x + y - 2} \right)$ là:
${\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} + 2xy \leqslant 32 $ $\Leftrightarrow {\left( {x + y} \right)^2} - 8\left( {x + y} \right) \leqslant 0 $ $\Leftrightarrow 0 \leqslant x + y \leqslant 8$
$A = {\left( {x + y} \right)^3} - 3\left( {x + y} \right) - 6xy + 6 $ $\geqslant {\left( {x + y} \right)^3} - \dfrac{3}{2}{\left( {x + y} \right)^2} - 3\left( {x + y} \right) + 6$
(do ${\left( {x + y} \right)^2} \geqslant 4xy $ $\Rightarrow xy \leqslant \dfrac{{{{\left( {x + y} \right)}^2}}}{4} $ $\Rightarrow - 6xy \geqslant - \dfrac{3}{2}{\left( {x + y} \right)^2}$ )
Xét hàm số $f\left( t \right) = {t^3} - \dfrac{3}{2}{t^2} - 3t + 6$ trên đoạn $\left[ {0,8} \right]$, ta có
$f'\left( t \right) = 3{t^2} - 3t - 3,f'\left( t \right) = 0 $ $\Leftrightarrow t = \dfrac{{1 \pm \sqrt 5 }}{2}$
(giá trị $\dfrac{{1 - \sqrt 5 }}{2} \notin \left[ {0;8} \right]$ nên loại)
Thực hiện tính toán ta có: $f\left( 0 \right) = 6,f\left( {\dfrac{{1 + \sqrt 5 }}{2}} \right) = \dfrac{{17 - 5\sqrt 5 }}{4},f\left( 8 \right) = 398 $
$\Rightarrow A \geqslant f\left( t \right) \geqslant \dfrac{{17 - 5\sqrt 5 }}{4} \Rightarrow A \geqslant \dfrac{{17 - 5\sqrt 5 }}{4}$
Vậy giá trị nhỏ nhất của $A$ là $\dfrac{{17 - 5\sqrt 5 }}{4}$ xảy ra khi $\left\{ \begin{gathered} x + y = \dfrac{{1 + \sqrt 5 }}{2} \hfill \\ x = y \hfill \\ \end{gathered} \right. \Leftrightarrow x = y = \dfrac{{1 + \sqrt 5 }}{4}$
Có bao nhiêu số nguyên \(m \in \left[ { - 5;5} \right]\) để \(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2\).
Xét hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + m\) trên \(\left[ {1;3} \right]\), có \(f'\left( x \right) = 3{x^2} - 6x,\,\,f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\left( L \right)\\x = 2\end{array} \right.\)
Bảng biến thiên:
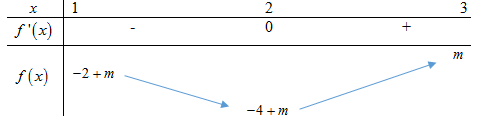
\(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2 \Rightarrow \left[ \begin{array}{l}m - 4 > 0\\m < 0\end{array} \right.\)
TH1: \(m - 4 > 0 \Leftrightarrow m > 4\)
\(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2 \Leftrightarrow m - 4 \ge 2 \Leftrightarrow m \ge 6\)
Mà \(m \in \left[ { - 5;5} \right] \Rightarrow m \in \emptyset \)
TH2: \(m < 0\)
\(\mathop {\min }\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \ge 2 \Leftrightarrow - m \ge 2 \Leftrightarrow m \le - 2\)
Mà \(m \in \left[ { - 5;5} \right],m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 5; - 4; - 3; - 2} \right\}\): 4 giá trị.
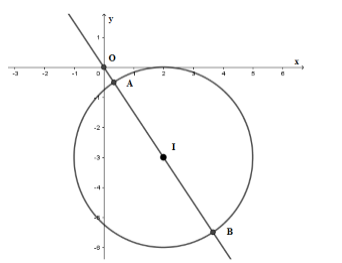
Cho hai số thực \(x,\,y\) thỏa mãn \({x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10} = \sqrt {6 + 4x - {x^2}} \). Gọi \(M,\,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(T = \left| {\sqrt {{x^2} + {y^2}} - a} \right|\). Có bao nhiêu giá trị nguyên thuộc đoạn \(\left[ { - 10;\,10} \right]\) của tham số \(a\) để \(M \ge 2m\)?
Ta có \({x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10} = \sqrt {6 + 4x - {x^2}} \)
\(\begin{array}{l} \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 + \sqrt {{y^2} + 6y + 10} - \sqrt {6 + 4x - {x^2}} = 0\\ \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 + \dfrac{{\left( {\sqrt {{y^2} + 6y + 10} - \sqrt {6 + 4x - {x^2}} } \right)\left( {\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} } \right)}}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }} = 0\end{array}\)
\(\begin{array}{l} \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 + \dfrac{{{y^2} + 6y + 10 - 6 - 4x + {x^2}}}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }} = 0\\ \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 + \dfrac{{{x^2} + {y^2} - 4x + 6y + 4}}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }} = 0\end{array}\)
\( \Leftrightarrow \left( {{x^2} + {y^2} - 4x + 6y + 4} \right)\left( {1 + \dfrac{1}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }}} \right) = 0\)
\( \Leftrightarrow {x^2} + {y^2} - 4x + 6y + 4 = 0\) (vì \(1 + \dfrac{1}{{\sqrt {{y^2} + 6y + 10} + \sqrt {6 + 4x - {x^2}} }} > 0\) )
\( \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\)
Phương trình \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\) là phương trình đường tròn \(\left( C \right)\) tâm \(I\left( {2; - 3} \right)\) và bán kính \(R = 3.\)
Gọi \(N\left( {x;y} \right) \in \left( C \right)\) ta suy ra \(ON = \sqrt {{x^2} + {y^2}} \) suy ra \(T = \left| {ON - a} \right|\)
Gọi \(A,B\) là giao điểm của đường tròn \(\left( C \right)\) và đường thẳng \(OI\).
Khi đó \(OA = OI - R = \sqrt {13} - 3\) và \(OB = OI + R = \sqrt {13} + 3\)
Suy ra \(\sqrt {13} - 3 \le \sqrt {{x^2} + {y^2}} \le \sqrt {13} + 3\)
TH1: Nếu \(\sqrt {13} - 3 \le a \le \sqrt {13} + 3\) thì \(\left| {\sqrt {{x^2} + {y^2}} - a} \right| \ge 0 \Rightarrow \min T = 0 \Rightarrow M \ge 2m \Rightarrow a \in \left\{ {1;2;3;4;5;6} \right\}\)
TH2: Nếu \(a < \sqrt {13} - 3 \Rightarrow a < \sqrt {13} \) nên \(\left| {\sqrt {13} + 3 - a} \right| > \left| {\sqrt {13} - 3 - a} \right|\), do đó \(M = \left| {\sqrt {13} + 3 - a} \right|;m = \left| {\sqrt {13} - 3 - a} \right|\)
Vì \(M \ge 2m \Rightarrow \left| {\sqrt {13} + 3 - a} \right| \ge 2\left| {\sqrt {13} - 3 - a} \right|\)
\( \Leftrightarrow {\left( {\sqrt {13} + 3 - a} \right)^2} - {\left( {2\sqrt {13} - 6 - 2a} \right)^2} \ge 0 \Leftrightarrow \sqrt {13} - 9 \le a \le \sqrt {13} - 1 \Rightarrow a \in \left\{ { - 5; - 4; - 3; - 2; - 1;0} \right\}\)
TH3: Nếu \(a > \sqrt {13} + 3 \Rightarrow a > \sqrt {13} \) nên \(\left| {\sqrt {13} + 3 - a} \right| < \left| {\sqrt {13} - 3 - a} \right|\), do đó \(m = \left| {\sqrt {13} + 3 - a} \right|;M = \left| {\sqrt {13} - 3 - a} \right|\)
Vì \(M \ge 2m \Rightarrow \left| {\sqrt {13} - 3 - a} \right| \ge 2\left| {\sqrt {13} + 3 - a} \right|\)
\( \Leftrightarrow {\left( {\sqrt {13} - 3 - a} \right)^2} - {\left( {2\sqrt {13} + 6 - 2a} \right)^2} \ge 0 \Leftrightarrow \sqrt {13} + 1 \le a \le \sqrt {13} + 9 \Rightarrow a \in \left\{ {7;8;9;10} \right\}\)
Vậy có 16 giá trị của \(a\) thỏa mãn đề bài.
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên
Bất phương trình \(f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\) nghiệm đúng với mọi \(x \in \left[ { - 1;3} \right]\) khi và chỉ khi:
\(\begin{array}{l}f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\,\,\forall x \in \left[ { - 1;3} \right] \Leftrightarrow g\left( x \right) = f\left( x \right) - \sin \dfrac{{\pi x}}{2} > m\,\,\forall x \in \left[ { - 1;3} \right]\\ \Rightarrow m < \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right)\end{array}\).
Từ đồ thị hàm số \(y = f'\left( x \right)\) ta suy ra BBT đồ thị hàm số \(y = f\left( x \right)\) như sau:
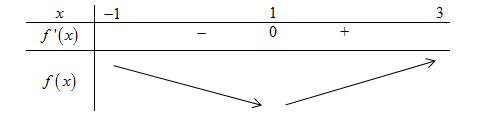
Dựa vào BBT ta thấy \(f\left( x \right) \ge f\left( 1 \right)\,\,\forall x \in \left[ { - 1;3} \right]\).
\(\begin{array}{l}x \in \left[ { - 1;3} \right] \Rightarrow \dfrac{{\pi x}}{2} \in \left[ { - \dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right] \Rightarrow - 1 \le \sin \dfrac{{\pi x}}{2} \le 1\\ \Leftrightarrow - 1 \le - \sin \dfrac{{\pi x}}{2} \le 1\end{array}\)
\( \Rightarrow f\left( 1 \right) - 1 \le f\left( x \right) - \sin \dfrac{{\pi x}}{2} \Leftrightarrow g\left( x \right) \ge f\left( 1 \right) - 1 \Rightarrow \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right) = f\left( 1 \right) - 1\).
Vậy \(m < f\left( 1 \right) - 1\).
Cho \(f\left( x \right) = \dfrac{1}{{{x^2} - 4x + 5}} - \dfrac{{{x^2}}}{4} + x\). Gọi \(M = \mathop {Max}\limits_{x \in \left[ {0;3} \right]} f\left( x \right);\) \(m = \mathop {Min}\limits_{x \in \left[ {0;3} \right]} f\left( x \right).\) Khi đó\(M-m\) bằng:
Ta có :
\[\begin{array}{l}f\left( x \right) = \dfrac{1}{{{x^2} - 4x + 5}} - \dfrac{{{x^2}}}{4} + x\\f\left( x \right) = \dfrac{1}{{{x^2} - 4x + 5}} - \dfrac{{{x^2} - 4x}}{4}\end{array}\]
Đặt \(t = {x^2} - 4x + 5\) với \(x \in \left[ {0;3} \right]\) ta có \(t' = 2x - 4 = 0 \Leftrightarrow x = 2 \in \left[ {0;3} \right]\).
Ta có : \(t\left( 0 \right) = 5;\,\,t\left( 2 \right) = 1,\,\,t\left( 3 \right) = 2\).
\( \Rightarrow \) Với \(x \in \left[ {0;3} \right]\) thì \(t \in \left[ {1;5} \right]\), khi đó hàm số trở thành \(f\left( t \right) = \dfrac{1}{t} - \dfrac{{t - 5}}{4}\) với \(t \in \left[ {1;5} \right]\).
Ta có \(f'\left( t \right) = - \dfrac{1}{{{t^2}}} - \dfrac{1}{4} < 0\,\,\forall t \in \left[ {1;5} \right]\).
\( \Rightarrow \) Hàm số \(y = f\left( t \right)\) nghịch biến trên \(\left[ {1;5} \right]\) \( \Rightarrow \left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ {0;3} \right]} f\left( x \right) = \mathop {\max }\limits_{\left[ {1;5} \right]} f\left( t \right) = f\left( 1 \right) = 2 = M\\\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = \mathop {\min }\limits_{\left[ {1;5} \right]} f\left( t \right) = f\left( 5 \right) = \dfrac{1}{5} = m\end{array} \right.\)
Vậy \(M - m = 2 - \dfrac{1}{5} = \dfrac{9}{5}\).
Cho hàm số \(f\left( x \right)\). Biết hàm số \(f'\left( x \right)\) có đồ thị như hình dưới đây. Trên đoạn \(\left[ { - 4;3} \right]\), hàm số \(g\left( x \right) = 2f\left( x \right) + {\left( {1 - x} \right)^2}\) đạt giá trị nhỏ nhất tại điểm
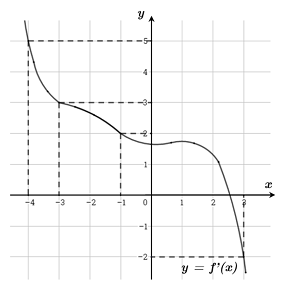
Ta có: \(g'\left( x \right) = 2f'\left( x \right) - 2\left( {1 - x} \right) = 2\left[ {f'\left( x \right) - \left( {1 - x} \right)} \right]\).
Xét \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = 1 - x\), số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và đường thẳng \(y = 1 - x\).
Ta biểu diễn đường thẳng \(y = 1 - x\) trên hình vẽ:
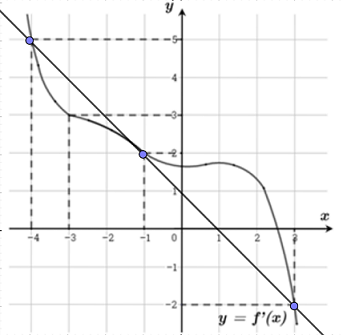
Dựa vào đồ thị hàm số ta thấy \(f'\left( x \right) = 1 - x \Leftrightarrow \left[ \begin{array}{l}x = - 4\\x = - 1\\x = 3\end{array} \right.\)
Từ đó, ta suy ra bảng xét dấu \(g'\left( x \right)\) như sau:
![]()
Vậy hàm số đạt GTNN tại \(x = - 1\).
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên:
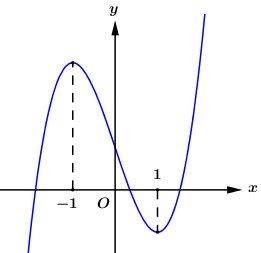
Giá trị nguyên lớn nhất của tham số m để hàm số \(y = f\left( {\left| x \right| - m} \right)\) đồng biến trên khoảng \(\left( {10; + \infty } \right)\) là:
Ta có \(y = f\left( {\left| x \right| - m} \right) = f\left( {\sqrt {{x^2}} - m} \right)\).
\( \Rightarrow y' = \dfrac{{2x}}{{2\sqrt {{x^2}} }}f'\left( {\sqrt {x^2} - m } \right) = \dfrac{x}{{\sqrt {{x^2}} }}f'\left( {\sqrt {x^2} - m } \right)\).
Để hàm số đồng biến trên \(\left( {10; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\).
\( \Rightarrow \dfrac{x}{{\sqrt {x^2} }}f'\left( {\sqrt {x^2} - m } \right) \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\) \( \Rightarrow f'\left( {\sqrt {x^2} - m} \right) \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\,\,\left( * \right)\).
Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên \(\left( {1; + \infty } \right)\) và \(\left( { - \infty ; - 1} \right)\).
Do đó \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}\sqrt {{x^2}} - m \ge 1\,\,\forall x \in \left( {10; + \infty } \right)\,\,\,\,\,\,\left( 1 \right)\\\sqrt {{x^2}} - m \le - 1\,\,\forall x \in \left( {10; + \infty } \right)\,\,\,\left( 2 \right)\end{array} \right.\)
Xét (1) ta có \(m \le \sqrt {{x^2}} - 1\,\,\forall x \in \left( {10; + \infty } \right) \Rightarrow m \le \mathop {\min }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} - 1} \right)\).
Xét \(g\left( x \right) = \sqrt {{x^2}} - 1\) trên khoảng \(\left( {10; + \infty } \right)\) ta có \(g'\left( x \right) = \dfrac{x}{{\sqrt {{x^2}} }} > 0\,\,\forall x \in \left( {10; + \infty } \right)\), do đó hàm số đồng biến trên \(\left( {10; + \infty } \right)\) \( \Rightarrow \mathop {\min }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} - 1} \right) = g\left( {10} \right) = 9 \Leftrightarrow m \le 9\).
Xét (2) ta có: \(m \ge \sqrt {{x^2}} + 1\,\,\forall x \in \left( {10; + \infty } \right)\) \( \Rightarrow m \ge \mathop {\max }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} + 1} \right)\).
Do \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2}} + 1} \right) = + \infty \) nên hàm số đã cho không có GTLN trên \(\left[ {10; + \infty } \right)\), do đó không tồn tại m thỏa mãn (2).
Vậy \(m \le 9\) nên giá trị nguyên lớn nhất của m bằng 9.
Cho hàm số \(y = {x^3} - 3m{x^2} + 3\left( {{m^2} - 1} \right)x + 2020\). Có tất cả bao nhiêu giá trị nguyên của tham số m sao cho hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\).
Ta có: \(y' = 3{x^2} - 6mx + 3\left( {{m^2} - 1} \right)\).
Cho \(y' = 0 \Leftrightarrow 3{x^2} - 6mx + 3\left( {{m^2} - 1} \right) = 0\) \( \Leftrightarrow {x^2} - 2mx + {m^2} - 1 = 0\).
Ta có \(\Delta ' = {m^2} - {m^2} + 1 = 1 > 0\), khi đó phương trình \(y' = 0\) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = m + 1\\{x_2} = m - 1\end{array} \right.\).
Ta có BBT:
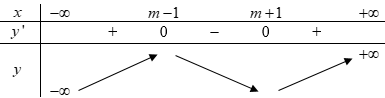
Ta có:
\(\begin{array}{l}f\left( {m - 1} \right) = {m^3} - 3m + 2022\\f\left( {m + 1} \right) = {m^3} - 3m + 2018\end{array}\)
TH1: \(0 < m - 1 \Leftrightarrow m > 1\).
Ta có: \(f\left( 0 \right) = 2020\).
Để hàm số có GTNN trên \(\left( {0; + \infty } \right)\) thì \(f\left( {m + 1} \right) \le f\left( 0 \right) \Leftrightarrow {m^3} - 3m + 2018 \le 2020\) \( \Leftrightarrow {m^3} - 3m - 2 \le 0\).
Xét hàm số \(f\left( m \right) = {m^3} - 3m - 2\) ta có \(f'\left( m \right) = 3{m^2} - 3 = 0 \Leftrightarrow m = \pm 1\),
BBT:
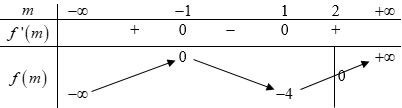
Dựa vào BT ta thấy \(f\left( m \right) \le 0 \Leftrightarrow m \le 2\).
Kết hợp điều kiện \( \Rightarrow 1 < m \le 2\).
TH2: \(m - 1 \le 0 < m + 1 \Leftrightarrow - 1 < m \le 1\), khi đó hàm GTNN của hàm số trên \(\left( {0; + \infty } \right)\) là \(f\left( {m + 1} \right)\).
Kết hợp 2 trường hợp ta có: \(\left[ \begin{array}{l}1 < m \le 2\\ - 1 < m \le 1\end{array} \right.\). Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1;2} \right\}\).
Vậy có 3 giá trị của m thỏa mãn yêu cầu bài toán.
Cho \(x,\,\,y\) là các số thực thỏa mãn \({2^{x + y - 1}}\left( {{3^{x + y}} + 1} \right) = 3x + 3y + 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = {x^2} + xy + {y^2}\).
Ta có:
\(\begin{array}{l}{2^{x + y - 1}}\left( {{3^{x + y}} + 1} \right) = 3x + 3y + 1\\ \Leftrightarrow {2^{x + y}}\left( {{3^{x + y}} + 1} \right) = 6x + 6x + 2\\ \Leftrightarrow {6^{x + y}} + {2^{x + y}} = 6\left( {x + y} \right) + 2\end{array}\)
Đặt \(x + y = t\), phương trình trở thành \({6^t} + {2^t} = 6t + 2\) \( \Leftrightarrow {6^t} + {2^t} - 6t - 2 = 0\)
Xét hàm số \(f\left( t \right) = {6^t} + {2^t} - 6t - 2\) ta có:
\(\begin{array}{l}f'\left( t \right) = {6^t}.\ln 6 + {2^t}.\ln 2 - 6\\f''\left( t \right) = {6^t}{\ln ^2}6 + {2^t}.{\ln ^2}2 > 0\,\,\,\forall t \in \mathbb{R}\end{array}\)
Do đó hàm số \(y = f'\left( t \right)\) đồng biến trên \(\mathbb{R}\), suy ra phương trình \(f'\left( t \right) = 0\) có nhiều nhất 1 nghiệm.
Suy ra phương trình \(f\left( t \right) = 0\) có nhiều nhất 2 nghiệm.
Ta lại có: \(\left\{ \begin{array}{l}f\left( 0 \right) = {6^0} + {2^0} - 6.0 - 2 = 0\\f\left( 1 \right) = {6^1} + {2^1} - 6.1 - 2 = 0\end{array} \right.\), do đó phương trình \(f\left( t \right) = 0\) có đúng hai nghiệm \(t = 0\), \(t = 1\).
\( \Rightarrow \left[ \begin{array}{l}x + y = 0\\x + y = 2\end{array} \right.\)
TH1: \(x + y = 0 \Rightarrow y = - x\).
Thay vào \(P\) ta có: \(P = {x^2} + xy + {y^2} = {x^2} \ge 0\).
TH2: \(x + y = 1 \Leftrightarrow y = 1 - x\).
Thay vào \(P\) ta có:
\(\begin{array}{l}P = {x^2} + x\left( {1 - x} \right) + {\left( {1 - x} \right)^2}\\=x^2-x+1\\= {\left( {x - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} \ge \dfrac{3}{4} \end{array}\).
Vậy giá trị nhỏ nhất của \(P\) là \(0\), đạt được khi \(x + y = 0\).

