Cho các số thực \(x,\,\,y\) thay đổi thỏa mãn \({x^2} + 2{y^2} + 2xy = 1\) và hàm số \(f\left( t \right) = {t^4} - {t^2} + 2\). Gọi \(M,\,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(Q = f\left( {\dfrac{{x + y + 1}}{{x + 2y - 2}}} \right)\). Tính \(M + m\)?
Ta có: \({x^2} + 2{y^2} + 2xy = 1 \Leftrightarrow {\left( {x + y} \right)^2} + {y^2} = 1\)
Đặt \(\left\{ \begin{array}{l}x + y = \sin \alpha \\y = {\rm{cos}}\alpha \end{array} \right.\). Ta có: \(Q = f\left( {\dfrac{{x + y + 1}}{{x + 2y - 2}}} \right) = f\left( {\dfrac{{\sin \alpha + 1}}{{\sin \alpha + {\rm{cos}}\,\alpha - 2}}} \right)\)
Đặt \(t = \dfrac{{\sin \alpha + 1}}{{\sin \alpha + {\rm{cos}}\,\alpha - 2}}\). Ta có: \(Q = f\left( {\dfrac{{\sin \alpha + 1}}{{\sin \alpha + {\rm{cos}}\,\alpha - 2}}} \right) = f\left( t \right)\)
\(t = \dfrac{{\sin \alpha + 1}}{{\sin \alpha + {\rm{cos}}\,\alpha - 2}}\,\,\left( {\alpha \in \mathbb{R}} \right) \Leftrightarrow t\sin \alpha + t{\rm{cos}}\,\alpha - 2t = \sin \alpha + 1 \Leftrightarrow \left( {t - 1} \right)\sin \alpha + t\,{\rm{cos}}\,\alpha = 2t + 1\) (*)
Để phương trình (*) tồn tại nghiệm \(\alpha \) thì \({\left( {t - 1} \right)^2} + {t^2} \ge {\left( {2t + 1} \right)^2}\)
\( \Leftrightarrow {t^2} - 2t + 1 + {t^2} \ge 4{t^2} + 4t + 1\)\( \Leftrightarrow 2{t^2} + 6t \le 0 \Leftrightarrow - 3 \le t \le 0\)
Xét \(Q = f\left( t \right) = {t^4} - {t^2} + 2\) trên đoạn \(\left[ { - 3;0} \right]\), có: \(f'\left( t \right) = 4{t^3} - 2t,\,\,f'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = \pm \sqrt {\dfrac{1}{2}} \end{array} \right.\)
Hàm số \(f\left( t \right)\) liên tục trên \(\left[ { - 3;0} \right]\), có \(f\left( { - 3} \right) = 74,\,f\left( { - \sqrt {\dfrac{1}{2}} } \right) = \dfrac{7}{4},\,f\left( 0 \right) = 2\)\( \Rightarrow \mathop {\min }\limits_{\left[ { - 3;0} \right]} f\left( t \right) = \dfrac{7}{4},\,\mathop {\max }\limits_{\left[ { - 3;0} \right]} f\left( t \right) = 74\)
\( \Rightarrow \)M + m\( = \dfrac{7}{4} + 74 = \dfrac{{303}}{4}\).
Cho hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\) có đồ thị là \(\left( C \right)\). Gọi \(M\left( {{x_M};{y_M}} \right)\) là một điểm bất kỳ trên \(\left( C \right)\). Khi tổng khoảng cách từ \(M\)đến hai trục tọa độ là nhỏ nhất, tính tổng \({x_M} + {y_M}\).
Đặt \(M\left( {x;\dfrac{{x + 1}}{{x - 1}}} \right) \in \left( C \right).\)
Khi đó ta có: \(\left\{ \begin{array}{l}d\left( {M;Ox} \right) = \left| {{y_M}} \right| = \left| {\dfrac{{x + 1}}{{x - 1}}} \right|\\d\left( {M;Oy} \right) = \left| {{x_M}} \right| = \left| x \right|\end{array} \right.\)
Tổng khoảng cách từ M đến hai trục tọa độ là \(S = \left| x \right| + \left| {\dfrac{{x + 1}}{{x - 1}}} \right| \ge \left| {x + \dfrac{{x + 1}}{{x - 1}}} \right|.\)
Dấu bằng xảy ra khi \(x.\dfrac{{x + 1}}{{x - 1}} \ge 0 \Leftrightarrow \left[ \begin{array}{l}x > 1\\ - 1 \le x \le 0\end{array} \right.\)
Đặt \(f\left( x \right) = x + \dfrac{{x + 1}}{{x - 1}} = \dfrac{{{x^2} + 1}}{{x - 1}}\)
\( \Rightarrow f'\left( x \right) = \dfrac{{{x^2} - 2x - 1}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 - \sqrt 2 \\x = 1 + \sqrt 2 \end{array} \right.\)
Bảng biến thiên:
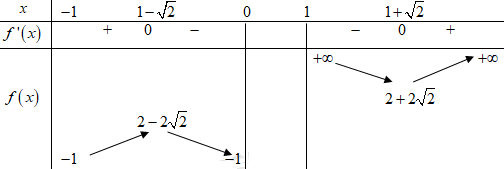
Dựa vào bảng biến thiên ta thấy \(\left| {x + \dfrac{{x + 1}}{{x - 1}}} \right| \ge \left| {2 - 2\sqrt 2 } \right| = 2\sqrt 2 - 2.\)
Dấu bằng xảy ra khi \(x = 1 - \sqrt 2 \Rightarrow y = 1 - \sqrt 2 \Rightarrow {x_M} + {y_M} = 2 - 2\sqrt 2 .\)
Đề thi THPT QG - 2021 - mã 101
Trên đoạn \(\left[ {0;3} \right]\), hàm số \(y = - {x^3} + 3x\) đạt giá trị lớn nhất tại điểm
Khảo sát hàm số \(y = - {x^3} + 3x\) trên \(\left[ {0;3} \right]\).
+ \(y' = - 3{x^2} + 3 = 0 \Leftrightarrow x = \pm 1\).
+ BBT:
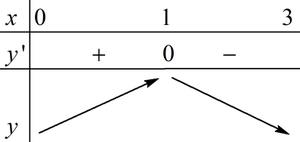
\( \Rightarrow \) Hàm số đạt giá trị lớn nhất tại \(x = 1\).
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như hình vẽ:
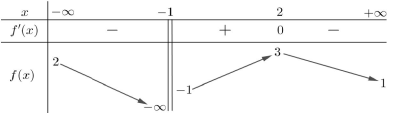
Tìm điều kiện của tham số \(m\) để \(m < f\left( x \right) + {x^2}\) với mọi \(x \in \left( {1;2} \right)\).
Đặt \(g\left( x \right) = f\left( x \right) + {x^2}\) ta có \(m < g\left( x \right)\,\,\forall x \in \left( {1;2} \right) \Leftrightarrow m \le \mathop {\min }\limits_{\left[ {1;2} \right]} g\left( x \right)\).
Ta có \(g'\left( x \right) = f'\left( x \right) + 2x\), với \(x \in \left( {1;2} \right)\)
Ta có \(\left\{ \begin{array}{l}f'\left( x \right) > 0\\2x > 0\end{array} \right. \Rightarrow g'\left( x \right) > 0\,\,\forall x \in \left( {1;2} \right)\).
\( \Rightarrow \) hàm số \(g\left( x \right)\) đồng biến trên \(\left( {1;2} \right)\).
\( \Rightarrow \mathop {\min }\limits_{\left[ {1;2} \right]} g\left( x \right) = g\left( 1 \right) = f\left( 1 \right) + 1\).
Vậy \(m \le f\left( 1 \right) + 1\).
Tính tổng tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số \(y = f(x) = \left| {2{x^3} - 15x + m - 5} \right| + 9x\) trên \(\left[ {0;3} \right]\) bằng 60.
6
6
6
Bước 1: Tìm m để \(\left| {2{x^3} - 15x + m - 5} \right| + 9x \le 60\)\(,\forall x \in [0;3]\)
Vì giá trị lớn nhất của hàm số \(y = f\left( x \right)\)trên đoạn [0; 3] bằng 60 nên ta có:
\(\left| {2{x^3} - 15x + m - 5} \right| + 9x \le 60\)\(,\forall x \in [0;3]\)
\( \Leftrightarrow \left| {2{x^3} - 15x + m - 5} \right| \le 60 - 9x\)\(,\forall x \in [0;3]\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2{x^3} - 15x + m - 5 \le 60 - 9x,}&{\forall x \in [0;3]}\\{2{x^3} - 15x + m - 5 \ge 9x - 60,}&{\forall x \in [0;3]}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \le - 2{x^3} + 6x + 65,\quad \forall x \in [0;3]}\\{m \ge - 2{x^3} + 24x - 55,\quad \forall x \in [0;3]}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \le {{\min }_{[0;3]}}\left( { - 2{x^3} + 6x + 65} \right)}\\{m \ge {{\max }_{[0;3]}}\left( { - 2{x^3} + 24x - 55} \right)}\end{array}} \right.\)
Dễ dàng tìm được \({\min _{[0;3]}}\left( { - 2{x^3} + 6x + 65} \right) = 29\) và \({\max _{[0;3]}}\left( { - 2{x^3} + 24x - 55} \right) = - 23\), do đó \( - 23 \le m \le 29.\)
Bước 2: Tính tổng các giá trị
Dấu bằng của phương trình \(f(x) = 60\) xảy ra khi và chỉ khi \(\left[ {\begin{array}{*{20}{l}}{m = 29}\\{m = - 23}\end{array}} \right.\).
Vậy có 2 giá trị thực của tham số \(m\) thỏa mãn yêu cầu và tổng của chúng bằng 6.
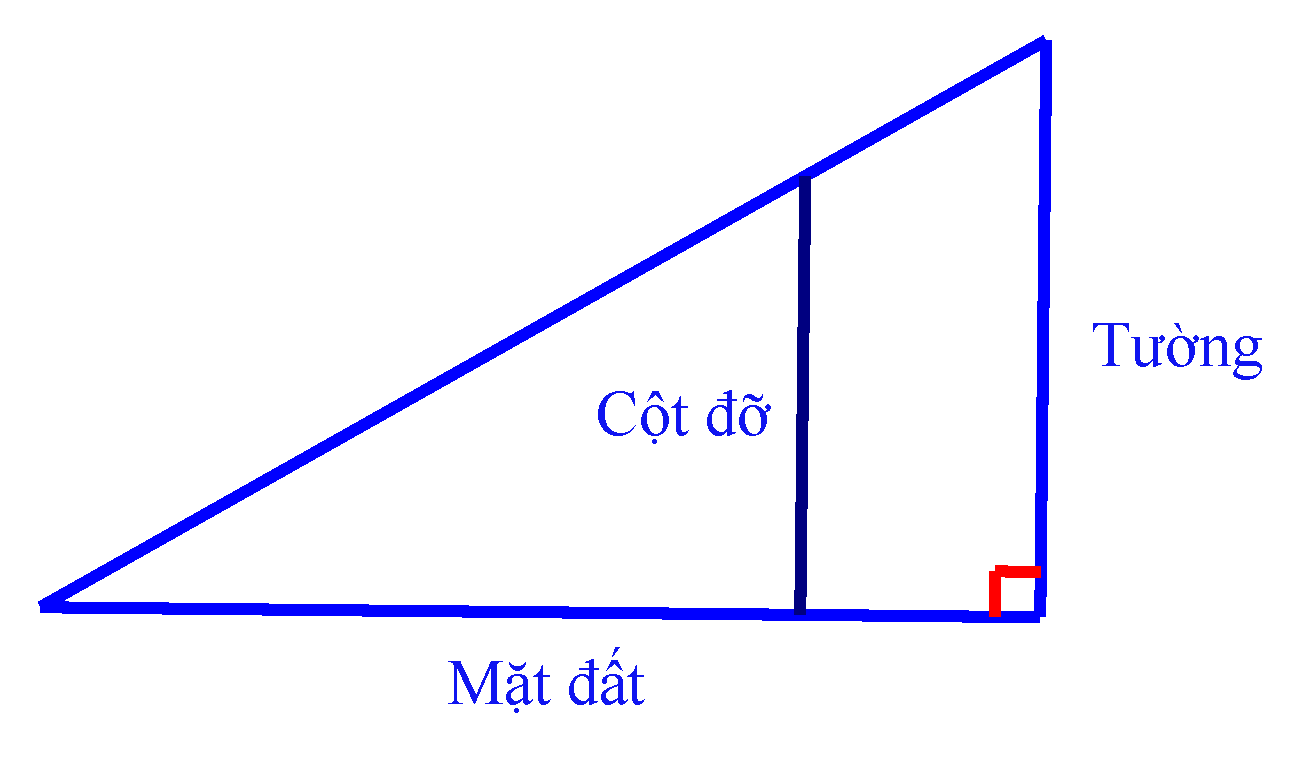
Tính chiều dài nhỏ nhất của cái thang để nó có thể dựa vào tường và bắc qua cột đỡ cao \(4\;{\rm{m}}\). Biết cột đỡ song song và cách tường \(0,5\;{\rm{m}}\), mặt phẳng chứa tường vuông góc với mặt đất, bỏ qua độ dày của cột đỡ.
\(\dfrac{{5\sqrt 5 }}{2}\)
\(\dfrac{{5\sqrt 5 }}{2}\)
\(\dfrac{{5\sqrt 5 }}{2}\)
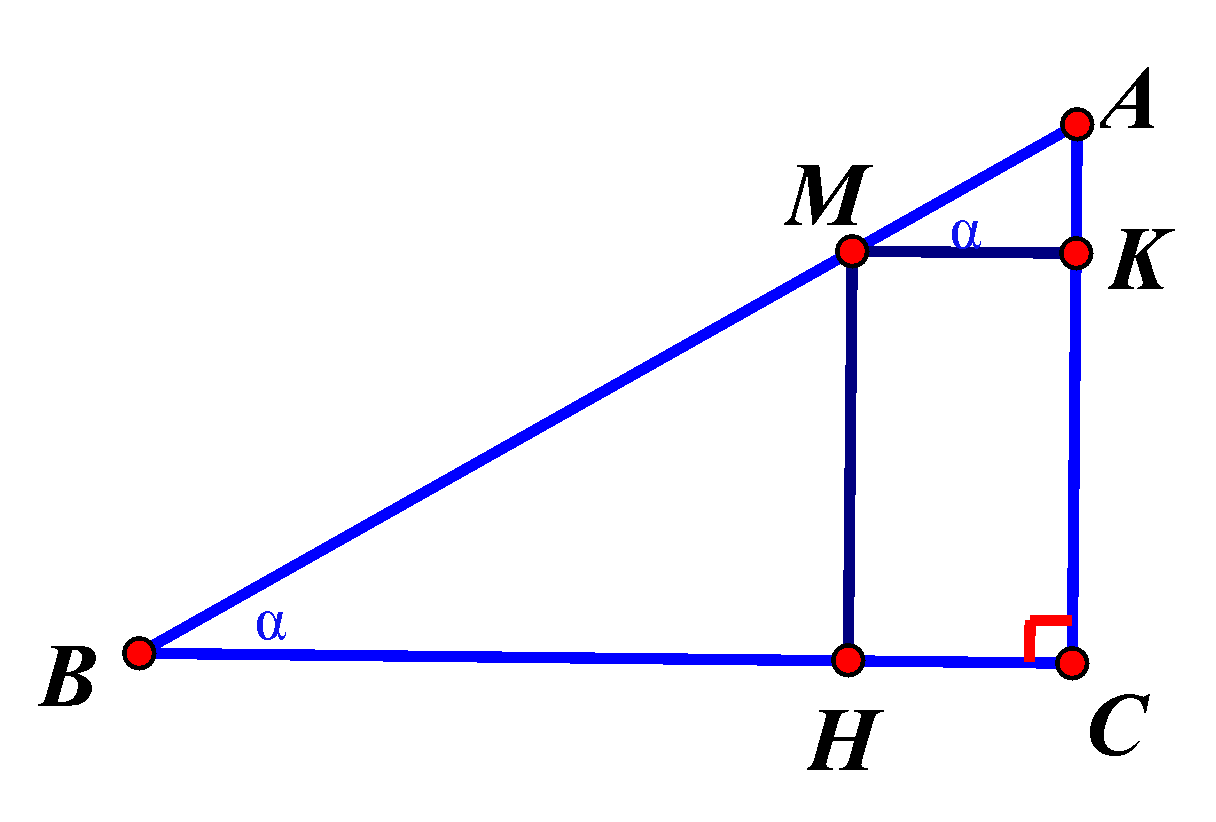
Bước 1: Đặt tên các điểm
Giả sử, ta đặt tên các điểm và góc như hình vẽ.
Ta có \(AM = \dfrac{1}{{2\cos \alpha }};MB = \dfrac{4}{{\sin \alpha }}\) với \(\alpha \in \left( {0;\dfrac{\pi }{2}} \right)\).
Bước 2: Tính min chiều dài của thang \(l\left( \alpha \right)\)
Chiều dài của thang là
\(l\left( \alpha \right) = AB = AM + MB\)\( = \dfrac{4}{{\sin \alpha }} + \dfrac{1}{{2\cos \alpha }}\)
\( \Rightarrow l'\left( \alpha \right) = \dfrac{{ - 8{{\cos }^3}\alpha + {{\sin }^3}\alpha }}{{2{{\sin }^2}\alpha .{{\cos }^2}\alpha }}\)
\( \Rightarrow l'(\alpha ) = 0\)\( \Leftrightarrow \tan \alpha = 2 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\sin \alpha = \dfrac{2}{{\sqrt 5 }}}\\{\cos \alpha = \dfrac{1}{{\sqrt 5 }}}\end{array}} \right.\)
Thay \(\sin \alpha = \dfrac{2}{{\sqrt 5 }}\) và \(\cos \alpha = \dfrac{1}{{\sqrt 5 }}\) vào \(l\left( \alpha \right)\) ta có:
\(l\left( \alpha \right) = 2\sqrt 5 + \dfrac{{\sqrt 5 }}{2} = \dfrac{{5\sqrt 5 }}{2}\)
Chiều dài nhỏ nhất của thang là \(\min l(\alpha ) = 2\sqrt 5 + \dfrac{{\sqrt 5 }}{2} = \dfrac{{5\sqrt 5 }}{2}\).
Một chiếc xe cứu hộ xuất phát từ góc của một hồ nước hình chữ nhật có các cạnh dài \(1600\;{\rm{m}}\) và rộng \(600\;{\rm{m}}\). Xe vừa có thể đi trên bờ hồ và đi trên mặt nước với vận tốc tương ứng là \(20\;{\rm{m}}/{\rm{s}}\) và \(12\;{\rm{m}}/{\rm{s}}\). Tính thời gian xe đi nhanh nhất đến tâm của hồ.

Đáp án:
s
Đáp án:
s
TH1: Đặt \(AM = x{\rm{. }}\)
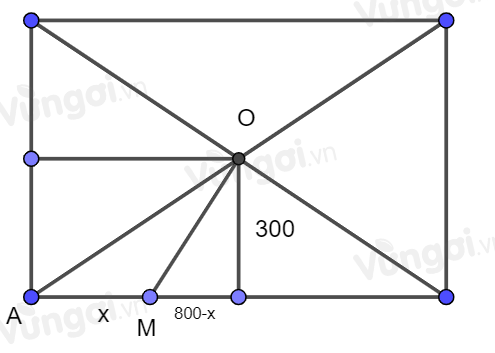
Xe cứu hộ đi theo hướng \({\rm{AMO }}\)
Thời gian đi của xe là:
\(t\left( x \right) = \dfrac{{AM}}{{20}} + \dfrac{{MO}}{{12}}\)
\( = \dfrac{x}{{20}} + \dfrac{{\sqrt {{{300}^2} + {{(800 - x)}^2}} }}{{{1^2}}}\)
\( = \dfrac{x}{{20}} + \dfrac{{\sqrt {{x^2} - 1600x + 730000} }}{{12}}\)
Ta có:
\({t^\prime }(x) = \dfrac{1}{{20}} + \dfrac{1}{{12}} \cdot \dfrac{{2x - 1600}}{{2\sqrt {{x^2} - 1600x + 730000} }} = 0\)
\( \Rightarrow x = 575\)
\( \Rightarrow {t_{\min }} = t(525) = 60{\rm{ (s)}}\)
TH2: Đặt \(AN = x\)
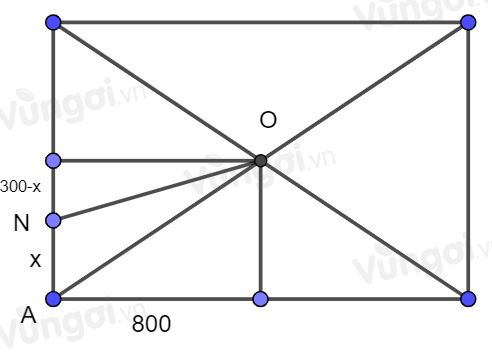
Xe cứu hộ đi theo hướng ANO.
Thời gian đi của xe là:
\(t\left( x \right) = \dfrac{{AN}}{{20}} + \dfrac{{NO}}{{12}}\)
\( = \dfrac{x}{{20}} + \dfrac{{\sqrt {{{800}^2} + {{(300 - 2)}^2}} }}{{12}}\)
\({t^\prime }(x) = 0 \Leftrightarrow x = - 300{\rm{ (s)}}\)(loại)
Vậy thời gian nhanh nhất xe đi đến tâm là 60(s).
Cho một tấm tôn hình vuông có cạnh bằng a. Người ta cắt 4 góc của tấm tôn để được một tấm tôn mới như hình vẽ.
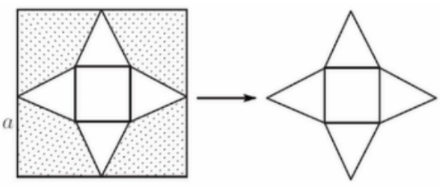
Từ tấm tôn mới, người ta gặp được một hình chóp tứ giác đều. Để khối chóp thu được có thể tích lớn nhất thì diện tích các miếng tôn bỏ đi là
Gọi x là độ dài của cạnh đáy của khối chóp
\(h\) là chiều cao của khối chóp, \(h'\) là chiều cao của tam giác cân ở mặt bên của khối chóp.
Bước 1: Biểu diễn h và thể tích V của khối chóp theo a và x
Ta có: \(x + 2h' = a\)\( \Rightarrow h' = \dfrac{{a - x}}{2}\)
Ta có: \({h^2} + {\left( {\dfrac{x}{2}} \right)^2} = {\left( {\dfrac{{a - x}}{2}} \right)^2}\) \( \Leftrightarrow h = \sqrt {{{\left( {\dfrac{{a - x}}{2}} \right)}^2} - {{\left( {\dfrac{x}{2}} \right)}^2}} = \dfrac{{\sqrt {{a^2} - 2ax} }}{2}\)
Thể tích khối chóp: \(V = \dfrac{1}{3}.\dfrac{{\sqrt {{a^2} - 2ax} }}{2}.{x^2}\)
\( = \dfrac{1}{6}\sqrt { - 2a{x^5} + {a^2}{x^4}} \)
Bước 2: Tìm max của \(f\left( x \right) = - 2a{x^5} + {a^2}{x^4}\) với x>0
Xét hàm số \(f\left( x \right) = - 2a{x^5} + {a^2}{x^4}\) với x>0
\({V_{\max }} \Leftrightarrow f{\left( x \right)_{\max }}\)
Ta có: \(f'\left( x \right) = - 10a{x^4} + 4{a^2}{x^3}\)
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{{2a}}{5}\end{array} \right.\)
\( \Rightarrow \max f\left( x \right) = f\left( {\dfrac{{2a}}{5}} \right) = \dfrac{{16{a^6}}}{{3125}}\)
Dấu “=” xảy ra khi và chỉ khi \(x = \dfrac{{2a}}{5}\)
Bước 3: Tìm phần diện tích bị bỏ
\( \Rightarrow\) Diện tích phần không bị bỏ là:
\(S = {x^2} + 4.\dfrac{1}{2}.x.\dfrac{{a - x}}{2} = \dfrac{{2{a^2}}}{5}\)
Diện tích bị bỏ là \(\dfrac{{3{a^2}}}{5}\)

