Câu hỏi:
2 năm trước
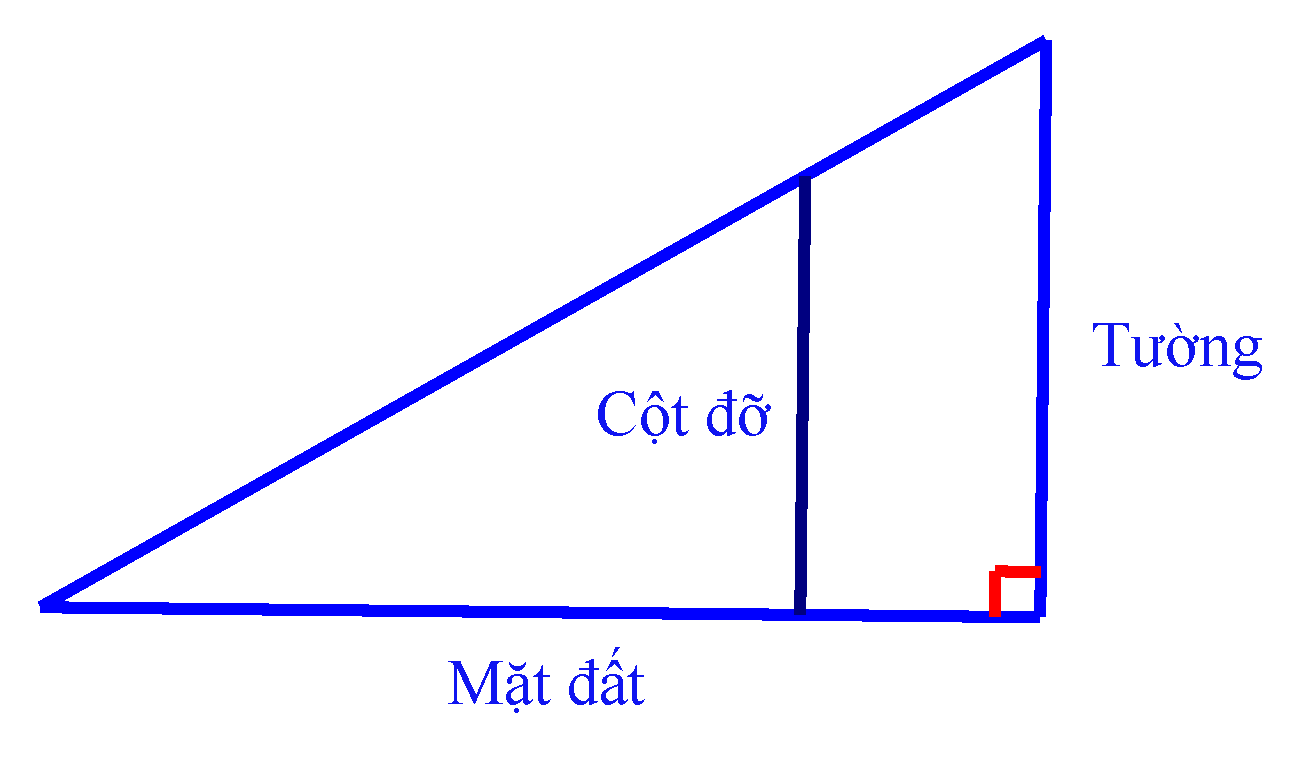
Tính chiều dài nhỏ nhất của cái thang để nó có thể dựa vào tường và bắc qua cột đỡ cao \(4\;{\rm{m}}\). Biết cột đỡ song song và cách tường \(0,5\;{\rm{m}}\), mặt phẳng chứa tường vuông góc với mặt đất, bỏ qua độ dày của cột đỡ.
Trả lời bởi giáo viên
Đáp án đúng:
\(\dfrac{{5\sqrt 5 }}{2}\)
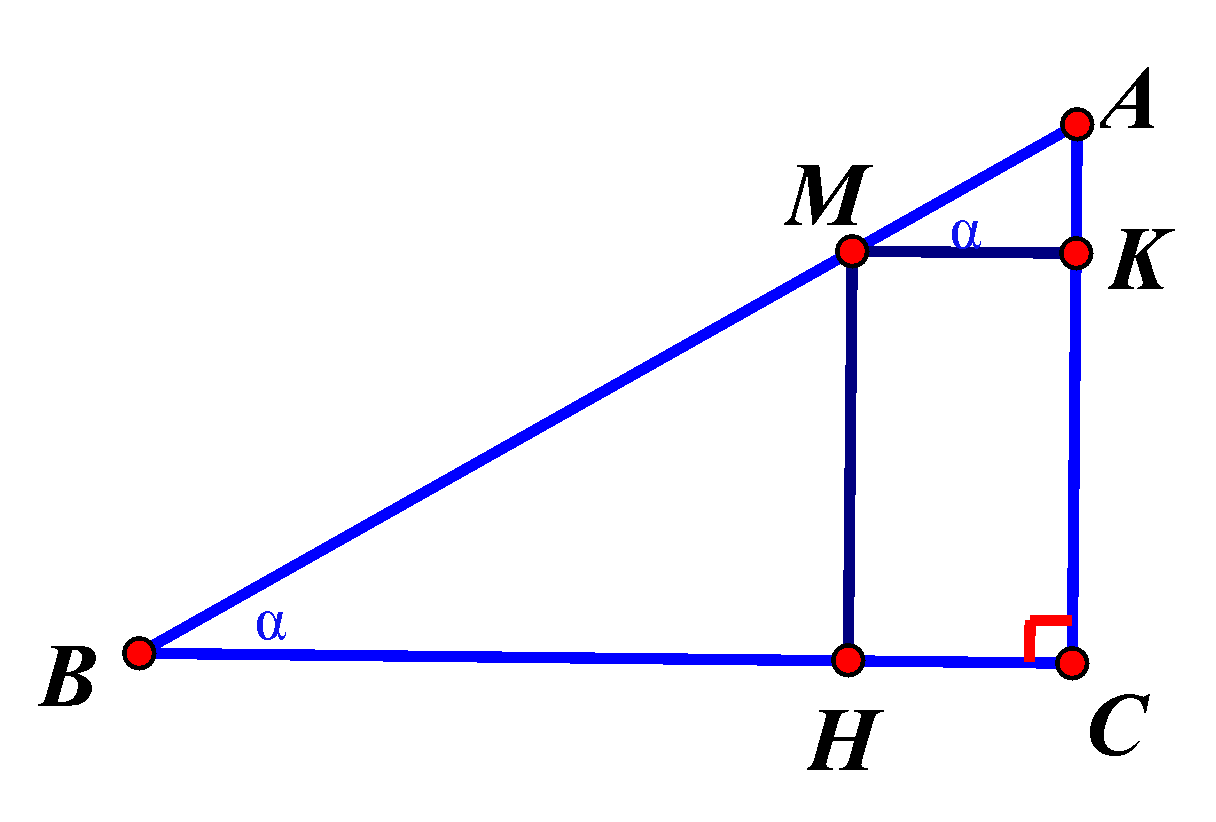
Bước 1: Đặt tên các điểm
Giả sử, ta đặt tên các điểm và góc như hình vẽ.
Ta có \(AM = \dfrac{1}{{2\cos \alpha }};MB = \dfrac{4}{{\sin \alpha }}\) với \(\alpha \in \left( {0;\dfrac{\pi }{2}} \right)\).
Bước 2: Tính min chiều dài của thang \(l\left( \alpha \right)\)
Chiều dài của thang là
\(l\left( \alpha \right) = AB = AM + MB\)\( = \dfrac{4}{{\sin \alpha }} + \dfrac{1}{{2\cos \alpha }}\)
\( \Rightarrow l'\left( \alpha \right) = \dfrac{{ - 8{{\cos }^3}\alpha + {{\sin }^3}\alpha }}{{2{{\sin }^2}\alpha .{{\cos }^2}\alpha }}\)
\( \Rightarrow l'(\alpha ) = 0\)\( \Leftrightarrow \tan \alpha = 2 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\sin \alpha = \dfrac{2}{{\sqrt 5 }}}\\{\cos \alpha = \dfrac{1}{{\sqrt 5 }}}\end{array}} \right.\)
Thay \(\sin \alpha = \dfrac{2}{{\sqrt 5 }}\) và \(\cos \alpha = \dfrac{1}{{\sqrt 5 }}\) vào \(l\left( \alpha \right)\) ta có:
\(l\left( \alpha \right) = 2\sqrt 5 + \dfrac{{\sqrt 5 }}{2} = \dfrac{{5\sqrt 5 }}{2}\)
Chiều dài nhỏ nhất của thang là \(\min l(\alpha ) = 2\sqrt 5 + \dfrac{{\sqrt 5 }}{2} = \dfrac{{5\sqrt 5 }}{2}\).
Hướng dẫn giải:
Bước 1: Đặt tên các điểm
Bước 2: Tính min chiều dài của thang \(l\left( \alpha \right)\)
- Giải phương trình \(l'\left( \alpha \right) = 0\).
- Tìm \(\sin \alpha ,\cos \alpha \).
- Thay vào tìm \(\min l\left( \alpha \right)\)
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
