Câu hỏi:
2 năm trước
Gọi \(M\) và \(m\) là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 2{\sin ^2}x - \cos x + 1\). Khi đó, giá trị của tổng \(M + m\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: a
\(\begin{array}{l}\,\,\,\,\,\,\,y = 2{\sin ^2}x - \cos x + 1\\ \Rightarrow y = 2\left( {1 - {{\cos }^2}x} \right) - \cos x + 1\\ \Rightarrow y = - 2{\cos ^2}x - \cos x + 3\end{array}\)
Đặt \(\cos x = t\,\,\,\,\left( { - 1 \le t \le 1} \right)\), hàm số trở thành: \(y = - 2{t^2} - t + 3.\)
Ta có: \(y' = - 4t - 1 = 0 \Rightarrow t = - \dfrac{1}{4}\,\,\,\left( {tm} \right)\).
Bảng biến thiên:
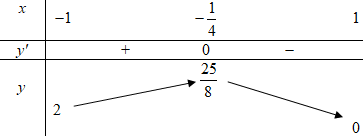
Từ BBT ta suy ra \(M = \dfrac{{25}}{8},\,\,m = 0\).
Vậy \(M + m = \dfrac{{25}}{8}\).
Hướng dẫn giải:
- Sử dụng công thức \({\sin ^2}x = 1 - {\cos ^2}x\).
- Đặt ẩn phụ \(t = \cos x\), điều kiện \(t \in \left[ { - 1;1} \right]\).
- Đưa hàm số về hàm số ẩn \(t\), tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 1;1} \right]\).
- Giải phương trình \(y' = 0\), xác định các nghiệm \({x_i} \in \left[ { - 1;1} \right]\).
- Tính các giá trị \(y\left( { - 1} \right),\,\,y\left( 1 \right),\,\,y\left( {{x_i}} \right)\).
- Kết luận: \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = \min \left\{ {y\left( { - 1} \right);y\left( 1 \right);y\left( {{x_i}} \right)} \right\}\), \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = \max \left\{ {y\left( { - 1} \right);y\left( 1 \right);y\left( {{x_i}} \right)} \right\}\).
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
